6

I would like to calculate the probability distribution of the sum of all the faces of $N$ dice rolls. The face probabilities ${p_i}$ are know, but are not $1 \over 6$. I have found answers for the case of a fair dice (i.e. $p_i={1 \over 6}$) here and here

For large $N$ I could apply the central limit theorem and use a normal distribution, but I don't know how to proceed for small $N$. (In particular, $N=2,4, 20$)

Community
  • 1
Ramon Crehuet
  • 173
  • Are you sure you know what you are asked to calculate? Please, tell us what have you already done and what are you trying to do. – V-X Feb 08 '16 at 15:17
  • 1
    I guess I simply want to know how the distribution in http://www.randomservices.org/random/apps/DiceExperiment.html is calculated. It's probably simple but I don't know how to do it. – Ramon Crehuet Feb 08 '16 at 16:14

3 Answers3

6

You can use generating functions.

Let $P=p_1x+p_2x^2+p_3x^3+p_4 x^4+p_5 x^5 +p_6 x^6$ where $p_i$ is the probability of $i$ occurring when rolling the die once.

Then the coefficient of $x^k$ in $P^N$ gives the probability of rolling a sum of $k$ when rolling the die $N$ times and summing.

For example, suppose $P=\frac{1}{7}x+\frac{1}{7}x^2+\frac{1}{7}x^3+\frac{1}{7}x^4+\frac{1}{7}x^5 + \frac{2}{7}x^6$.

Then, using a computer algebra system (I like PARI/GP), we find $P^3 = \frac{8}{343} x^{18} + \frac{12}{343} x^{17} + \frac{18}{343} x^{16} + \frac{25}{343} x^{15} + \frac{33}{343} x^{14} + \frac{6}{49} x^{13} + \frac{40}{343} x^{12} + \frac{39}{343} x^{11} + \frac{36}{343} x^{10} + \frac{31}{343} x^9 + \frac{24}{343} x^8 + \frac{15}{343} x^7 + \frac{10}{343} x^6 + \frac{6}{343} x^5 + \frac{3}{343} x^4 + \frac{1}{343} x^3$.

From this, we can conclude, for instance, that the probability of a sum of $10$ when rolling $3$ times (or rolling once with three identical copies of this die) is $\frac{36}{343}.$

(Using Bruce's example, we get $P^3=\frac{1}{64} x^{18} + \frac{3}{64} x^{17} + \frac{3}{32} x^{16} + \frac{1}{8} x^{15} + \frac{9}{64} x^{14} + \frac{9}{64} x^{13} + \frac{25}{192} x^{12} + \frac{7}{64} x^{11} + \frac{5}{64} x^{10} + \frac{91}{1728} x^9 + \frac{19}{576} x^8 + \frac{11}{576} x^7 + \frac{1}{108} x^6 + \frac{1}{288} x^5 + \frac{1}{576} x^4 + \frac{1}{1728} x^3$, and so the probability of $10$ is $\frac{5}{64}=0.078125$ (exactly).)

Matthew Conroy
  • 11,234
  • 1
    Nice approach. But are you sure of your answer for a sum of ten? After my initial simulation mean(t == 10) returns 0.078097, whereas $36/343 \approx 0.1049563.$ Too far away. – BruceET Feb 08 '16 at 18:21
  • 1
    OK, we're using differently biased dice. With your bias, I get 0.104877 for a total of 10 and 0.02338 for a total of 18. Got rid of one of by Comments to simplify for readers. – BruceET Feb 08 '16 at 18:54
  • As a curiosity, do you have any idea of how could this be implemented in this applet http://www.randomservices.org/random/apps/DiceExperiment.html I am pretty sure the algebra system is not part of it... – Ramon Crehuet Feb 09 '16 at 09:09
  • 1
    @RamonCrehuet: Couldn't be sure without looking at the code. Doubt if simulation. Probably, programming successive convolutions one step at a time of the simple discrete distributions. (In my browser this link is partially broken). – BruceET Feb 09 '16 at 18:26
3

It seems to me the spirit of the original context is experimental. In order to get an analytic answer, even in a simple case with only two rolls, you need to specify precisely how the die is loaded.

Here is a simulation in R of an experiment with $n = 3$ rolls of a die loaded so that faces 1 to 6 appear with probabilities $(1/12, 1/12, 1/12, 3/12, 3/12, 3/12)$. In practice, such a bias might be achieved by embedding a heavy weight just below the corner where faces 1, 2, and 3 meet. A million three-roll experiments are simulated. Each pass through the loop simulates one three-roll experiment. The random variable $T$ is the total on the three dice (values between 3 and 18, inclusive).

For the mean and SD of the best-fitting normal distribution, you should be able to find $E(T) = 12.75$ and $SD(T) = ?$, which are approximated in the simulation. (Also, the exact computation is shown for $E(T) = n\sum_{i=1}^6 ip_i.$)

 m = 10^6;  n = 3;  p = c(1, 1, 1, 3, 3, 3)/12
 t = numeric(m) # vector to receive totals
 for (i in 1:m) {
   faces = sample(1:6, n, repl=T, prob = p)
   t[i] = sum(faces)  }
 mean(t);  sd(t)
 ## 12.74981  # Approx E(T) = 12.75
 ## 2.657790  # Approx SD(T)
 hist(t, br=(2:18)+.5, prob=T, main="Sum of 3 Rolls", col="wheat", ylim=c(0,.15))
 curve(dnorm(x, mean(t), sd(t)), lwd=2, col="blue", add=T)
 3*sum((1:6)*p)
 ## 12.75     # Exact E(T)

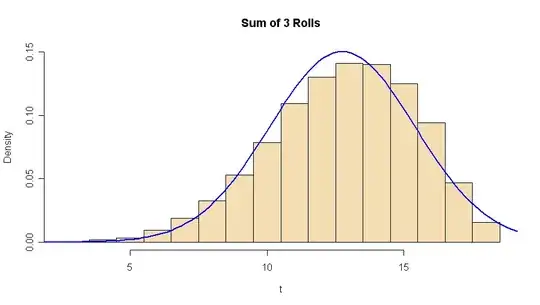
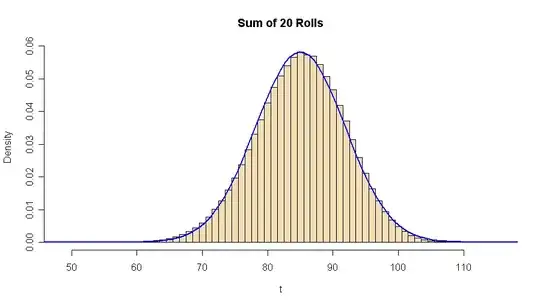
enter image description here

The normal curve with matching mean and SD is not yet a good fit for only three rolls. Perhaps much better for 20. Using code $mutatis\;mutandis$: Yes 20 looks better. enter image description here

BruceET
  • 51,500
  • Might want to browse 'related' pages shown in the right margin for some some interesting combinatorics. – BruceET Feb 08 '16 at 18:05
1

As an alternative to Matthew Conroy's suggestion to use a computer algebra system, one can also code this with Python using numpy class of Polynomials. The convolution power can be simply obtained by calculating the power of a polynomial. The same example he suggests can be coded as follows:

In [14]: from numpy.polynomial.polynomial import Polynomial

In [15]: p=Polynomial((1/7, 1/7, 1/7, 1/7,1/7, 2/7))

In [16]: p**3  # or alternatively: np.power(p,3)
Out[16]: 
Polynomial([ 0.00291545,  0.00874636,  0.01749271,  0.02915452,  0.04373178,
        0.06997085,  0.09037901,  0.10495627,  0.11370262,  0.11661808,
        0.12244898,  0.09620991,  0.0728863 ,  0.05247813,  0.03498542,
        0.02332362], [-1.,  1.], [-1.,  1.])

Of course, one has to work with floats, but otherwise the results agree.

In numpy, the convolution can also be coded with np.convolve , but the application of successive convolutions is more cumbersome.

Ramon Crehuet
  • 173