9

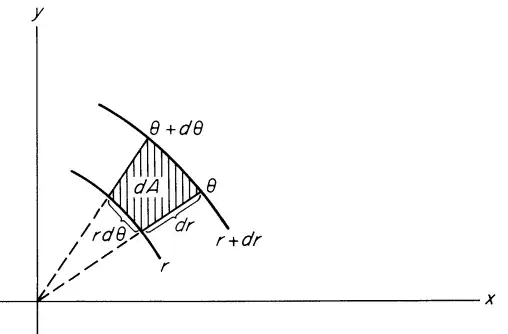
$x = r \cos \theta$, $y = r \sin \theta$

I got $dx = \cos \theta dr - r \sin \theta d \theta $

$ dy = \sin \theta dr + r \cos \theta d \theta$

How to get $dx dy = r dr d \theta$??

I saw the same question Rigorous proof that $dx dy=r\ dr\ d\theta$.

But I am not getting where vectors are coming in to the picture thanks.

Community
  • 1
user304876
  • 119
  • 2
    The more advanced point of view: the Jacobian determinant of that change of variables is $r$. – GEdgar Feb 15 '16 at 16:18
  • 2
    If you take the exterior product of $dx$ and $dy$ you get the desired result. But you may not know how to do that. – Matt Samuel Feb 15 '16 at 16:28
  • why the simple product of $dx$ and $dy$ doesn't give $r dr d\theta?$ – user304876 Feb 16 '16 at 06:20
  • @user304876: The equation dxdy is for orthogonal basis. On the other hand if y=f(x), a different result is found: xdy/dx−y=(x2+y2)dθ/dx; where, Tanθ=y/x, R^2=x^2+y^2, (alternatively Tanθ=x/y , depending on the absolute value of the RHS, an abstraction). This equation is nifty, simple. Easily proven from the definitions of x=Rcos(x), y=Rsin(x). Enjoy. – 926reals Nov 21 '16 at 02:23
  • Kindly view this link. dx dy represents area vectr which is cross product. https://www.math.wisc.edu/~lmao/2014_fall_teach/notes_pollar_coordinate.pdf – user520111 Jan 10 '18 at 00:44
  • This answer might shed some light on this question. – robjohn Jan 23 '22 at 17:50

3 Answers3

5

How to get $dx\;dy=r\;dr\;dθ$?

I suggest you take a look at Advanced calculus of several variables by C.H. Edwards. In Section 5 of Chapter IV, we can read something like this:

The student has undoubtedly seen change of variables formulas such as $$\iint f(x,y)\;dx\;dy=\iint f(r\cos\theta,r\sin\theta)\;r\;dr\;d\theta$$ which result from changes from rectangular coordinates to polar coordinates. The appearance of the factor $r$ in the formula is sometimes "explained" by mythical pictures, such as figure below, in which it is alleged that $dA$ is an "infinitesimal" rectangle with sides $dr$ and $r\;d\theta$, and therefore has area $r \;dr\; d\theta$. In this section we shall give a mathemtaically acceptable explanation of the origin of such factors in the transformation of multiple integrals from one coordinate system to another.

enter image description here

EDIT

For details about the Edwards approach, I refer the reader to this post.

Community
  • 1
Pedro
  • 18,817
  • 7
  • 65
  • 127
  • 3
    This isn't really an answer as it stands; answer should be self contained, but this answer lacks the "mathematically acceptable explanation" it alludes to, so it's not very useful. If you're going to reproduce anything from a book, you might as well reproduce the part that answers the question rather than the part that asks the questions. – Milo Brandt Feb 16 '16 at 02:55
  • @MiloBrandt In my opinion, the said book is a good source on the subject and the reproduced quote motivates the reading. This is why I have written this post. I hope my edit meets your demands. – Pedro Feb 16 '16 at 20:31
4

A piece of an annulus swept out by a change of angle $\Delta \theta$ and a change of radius $\Delta r$, starting from a point given by $(r,\theta)$, has area $\Delta \theta \int_r^{r+\Delta r} s ds = \Delta \theta \frac{(r+\Delta r)^2-r^2}{2} = \Delta \theta \left ( r \Delta r + \frac{\Delta r^2}{2} \right )$. (This is computed by integrating the length of circular arcs.)

As $\Delta r \to 0$ the second term is asymptotically much smaller than the first, which heuristically justifies the change of variables formula. Showing that this procedure, which is equivalent to the more general procedure based on the Jacobian determinant, actually makes integrals do the correct thing takes some more work. The details can be found in a typical undergraduate real analysis text.

Ian
  • 101,645
0

It is not so complicated. At first, direct multiplication of your two right hand quantities and simplification gives the result!

EDIT1:

Differential/infinitesmal area as an approximation in the following, is reckoned as:

$$ d\theta \,(R_o+R_i)/2 \approx dy,\, (R_o -R_i) \approx dx,\, A \approx dx \, dy $$

DifferentialTriangleArea

And secondly/basically (geometrically) what we mean by area directly is by differential lengths multiplication of a rectangle sides of length $ dx \approx dr $ and height $ dy \approx r d\theta $ which should be appreciated by definition.

Narasimham
  • 40,495