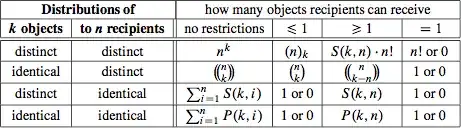
Let $S$ be a set of $n \in \mathbb{N}$ elements.
e.g. $\{1,2,3\}~~n \leftarrow 3$
1. Permutations ($n!$)
Ordered without repetition.
Also called (re-)arrangement, (re-)ordering or substitutions.
The "passive" way to regard a permutation of the set S is an ordered arrangement (or listing, or linearly ordered arrangement, or sequence without repetition) of the elements of S
That would be the bijections from $S$ to itself.
e.g. $\{(1,2,3), (1,3,2), (2,1,3), (3,2,1), (2,3,1), (3,1,2)\}$ (each can be found in $S^n$)
2. multiset permutations ($\frac{n!}{\prod{k_i!}}$)
Ordered but with "limited" repetitions :
if $M$ is a finite multiset, then a multiset permutation is an ordered arrangement of elements of $M$ in which each element appears exactly as often as is its multiplicity in $M$.
e.g. with $M=\{1, 1, 2, 3, 3, 3\}$ we would have $(k_1,k_2,k_3)\leftarrow(2,1,3)$ and therefore the number of possible multiset permutations would be $\frac{Card(M)!}{k_1!.k_2!.k_3!}=\frac{6!}{2!1!3!}$
$$\text{let} (k_1,k_2,\dots,k_i) \in (\mathbb{N}^*)^i ~~~~ \sum_{p=1}^{i}{k_p} = n$$
the number of multiset permutations is $$\frac{|M|!}{\prod_{p=1}^{i}{k_p!}}$$
3. k-permutations ($\frac{n!}{(n-k)!}$)
Ordered without repetition
"Weaker" than permutations, it is ordered but with the number of chosen elements being $k\leqslant n$
These are not permutations except in special cases, but are natural generalizations of the ordered arrangement concept.
e.g. for $k\leftarrow 2$ : {(1,2),(2,3),(1,3),(2,1),(3,1),(3,2)}
(each can be found in $S^k$)
Sometimes called variations in the older literature, these objects are also known as partial permutations or as sequences without repetition, terms that avoid confusion with the other, more common, meaning of "permutation"
0 if k > n
4. k-tuples ($n^k$)
Ordered with repetition
Ordered arrangements of length k of the elements of a set $S$ where repetition is allowed are called k-tuples, but have sometimes been referred to as permutations with repetition although they are not permutations in general. They are also called words over the alphabet $S$ in some contexts.
A k-tuple is a sequence (or ordered list) of k elements ($k\in\mathbb{N}$)
e.g. for $k\leftarrow 2 : \{(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)\}$
I personally see it as writing in base $n$ with the character set $S$
5. k-combinations ($\binom{n}{k}$)
Unordered without repetition
combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter.
A k-combination of a set $S$ is a subset of k distinct elements of $S$.
0 if k > n
6. k-multicombination ($\binom{n+k-1}{k}$)
Unordered with repetition
k-combination with repetitions or k-multicombination, or multisubset
Combinations refer to the combination of n things taken k at a time without repetition. To refer to combinations in which repetition is allowed, the terms k-selection, k-multiset, or k-combination with repetition are often used.
Sum Up
| | Ordered | Unordered |
|------------|----------------------------|--------------------|
| Repetition | k-tuples | k-multicombination |
| Uniqueness | permutation, k-permutation | k-combinations |
Source
Wikipedia/Permutation and Wikipedia/Combination