Finding shortest distance between a point and a surface

Question

Consider the surface $S$ (in $\mathbb R^3$) given by the equation $z=f(x,y)=\frac32(x^2+y^2)$. How can I find the shortest distance from a point $p=(a,b,c)$ on $S$ to the point $(0,0,1)$.

This is what I have done: Define $d(a,b,c)=a^2+b^2+(c-1)^2$, for all points $p=(a,b,c)\in S$. Then $\sqrt d$ is the distance from $S$ to $(0,0,1)$. I think that the method of Lagrange multipliers is the easiest way to solve my question, but how can I find the Lagrangian function? Or is there an easier way to find the shortest distance?

Answer 1

I think that the method of Lagrange multipliers is the easiest way to solve my question, but how can I find the Lagrangian function?

As shown by other answers and in note 1 there are easier ways to find the shortest distance, but here is a detailed solution using the method of Lagrange multipliers. You need to find the minimum of the distance function

$$\begin{equation} d(x,y,z)=\sqrt{x^{2}+y^{2}+(z-1)^{2}} \tag{1a} \end{equation}$$

subject to the constraint given by the surface equation $z=f(x,y)=\frac32(x^2+y^2)$ $$\begin{equation} g(x,y,z)=z-\frac{3}{2}\left( x^{2}+y^{2}\right) =0. \tag{2} \end{equation}$$ Since $\sqrt{x^{2}+y^{2}+(z-1)^{2}}$ increases with $x^{2}+y^{2}+(z-1)^{2}$ you can simplify the computations if you find the minimum of $$\begin{equation} [d(x,y,z)]^2=x^{2}+y^{2}+(z-1)^{2} \tag{1b} \end{equation}$$ subject to the same constraint $(2)$. The Lagrangian function is then defined by $$\begin{eqnarray} L\left( x,y,z,\lambda \right) &=&[d(x,y,z)]^2+\lambda g(x,y,z) \\ L\left( x,y,z,\lambda \right) &=&x^{2}+y^{2}+(z-1)^{2}+\lambda \left( z- \frac{3}{2}\left( x^{2}+y^{2}\right) \right), \tag{3} \end{eqnarray}$$ where $\lambda $ is the Lagrange multiplier. By this method you need to solve the following system $$\begin{equation} \left\{ \frac{\partial L}{\partial x}=0,\frac{\partial L}{\partial y}=0, \frac{\partial L}{\partial z}=0,\frac{\partial L}{\partial \lambda } =0,\right. \tag{4} \end{equation}$$ which results in

$$\begin{eqnarray} \left\{ \begin{array}{c} 2x+3\lambda x=0 \\ 2y+3\lambda y=0 \\ 2z-2-\lambda =0 \\ -z+\frac{3}{2}\left( x^{2}+y^{2}\right) =0 \end{array} \right. &\Leftrightarrow &\left\{ \begin{array}{c} x=0\vee 2+3\lambda =0 \\ y=0\vee 2+3\lambda =0 \\ 2z-2-\lambda =0 \\ -z+\frac{3}{2}\left( x^{2}+y^{2}\right) =0 \end{array} \right. \\ &\Leftrightarrow &\left\{ \begin{array}{c} x=0 \\ y=0 \\ \lambda =2 \\ z=0 \end{array} \right. \vee \left\{ \begin{array}{c} \lambda =-2/3 \\ z=2/3 \\ x^{2}+y^{2}=4/9 \end{array} \right. \tag{5} \end{eqnarray}$$

For $x=y=x=0$ we get $d(0,0,0)=1$. And for $x^2+y^2=4/9,z=2/3$ we get the minimum distance subject to the given conditions $$\begin{equation} \underset{g(x,y,z)=0}\min d(x,y,z)=\sqrt{\frac{4}{9}+(\frac{2}{3}-1)^{2}}=\frac{1}{3}\sqrt{5}. \tag{6} \end{equation}$$

It is attained on the intersection of the surface $z=\frac{3}{2}\left( x^{2}+y^{2}\right) $ with the vertical cylinder $x^{2}+y^{2}=\frac{4}{9}$ or equivalently with the horizontal plane $z=\frac{2}{3}$.

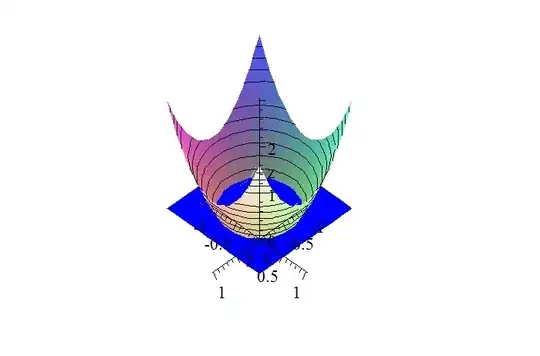$$\text{Plane }z=\frac{2}{3} \text{(blue) and surface }z=\frac{3}{2}\left( x^{2}+y^{2}\right) $$

Notes.

1. As the solution depends only on the sum $r^{2}=x^{2}+y^{2}$ we could just find $$\begin{equation} \min [d(r)]^2=r^{2}+(\frac{3}{2}r^{2}-1)^{2} \tag{7} \end{equation}$$ and then find $d(r)=\sqrt{[d(r)]^2}$ at the minimum.
2. The surface $z=\frac{3}{2}\left( x^{2}+y^{2}\right) $ is a surface of revolution around the $z$ axis.

Answer 2

Let $q=(a,b,c)$ be the one of the closest to $p$ point of $S$. Since $q\in S$ we have $$ c=\frac{3}{2}(a^2+b^2)\tag{1} $$ On the other hand the vector $pq=(a,b,c-1)$ is orthogonal to $S$ (because $q$ is the closest to $p$ point of $S$), hence $pq$ is collinear to the normal $n$ to the surface $S$ at the point $q$. This normal is easily computable $$ n=(-3a,-3b,1) $$ Since $pq$ and $n$ are collinear vectors $$ \frac{-3a}{a}=\frac{-3b}{b}=\frac{1}{c-1}\tag{2} $$ The rest is clear.

Answer 3

Here's another approach. The distance between the surface and the point can be expressed solely in terms of $r=\sqrt{x^2+y^2}$, $$d(r) = \sqrt{1-2 r^2+\frac{9}{4} r^4}.$$ Extremizing $d(r)$ with respect to $r$ we find $$r\left(r^2-\frac{4}{9}\right) = 0,$$ so $r=0$ or $r=2/3$. But $d(0) = 1$ and $d(2/3) = \sqrt{5}/3$. Thus, the shortest distance between the point and the surface is $\sqrt{5}/3$. This is the distance between the point and the circle $(x,y,\frac{3}{2}r^2) = (x,y,2/3)$, where $x^2+y^2 = 4/9$.

Answer 4

The Lagrangian is $L(x,y,z,\lambda)=d(x,y,z)+\lambda(z-\frac32(x^2+y^2))$. Compute the partial derivatives of $L$ with respect to $x,y,z$ and $\lambda$. Setting all the partial derivatives equal to $0$ gives $x=y=0, z=\frac32(x^2+y^2)$ and $\lambda=\frac23$. This gives critical points $(0,0,0)$ and $(0,0,\frac23)$. Plugging these points into $d$ gives the minimal distance from a point on $S$ to $(0,0,1)$.

Answer 5

Let $d = a^2 + b^2$ and,

$$f(d) = a^2 + b^2 + (c-1)^2 = d + \left ( \frac{3}{2}d -1 \right )^2.$$

Thus, setting $f'(d) = (9/2)d-2 = 0$ gives us the critical point $d^* = 4/9$ and so, $$f(d^*) = \frac{5}{9}.$$

Hence, the distance you're looking for is $$\sqrt{f(d^*)} = \frac{\sqrt{5}}{3}.$$