(Elegant) proof of : $x \log_2\frac{1}{x}+(1-x) \log_2\frac{1}{1-x} \geq 1- (1-\frac{x}{1-x})^2$

Question

I am looking for the most concise and elegant proof of the following inequality: $$ h(x) \geq 1- \left(1-\frac{x}{1-x}\right)^2, \qquad \forall x\in(0,1) $$ where $h(x) = x \log_2\frac{1}{x}+(1-x) \log_2\frac{1}{1-x}$ is the binary entropy function. Below is a graph of the two functions.

Of course, an option would be to differentiate $1,2,\dots,k$ times, and study the function this way — it may very well work, but is not only computationally cumbersome, it also feels utterly inelegant. (For my purposes, I could go this way, but I'd rather not.)

I am looking for a clever or neat argument involving concavity, Taylor expansion around $1/2$, or anything — an approach that would qualify as "proof from the Book."

Answer 1

I do not think that this is elegant enough.

Considering $$ h(x) = x \log_2\frac{1}{x}+(1-x) \log_2\frac{1}{1-x}$$ $$g(x)=1- \left(1-\frac{x}{1-x}\right)^2$$ $$f(x)=h(x)-g(x)$$ Expanding $f(x)$ as a Taylor series built at $x=\frac 12$, the result is $$f(x)= \left(16-\frac{2}{\log (2)}\right)\left(x-\frac{1}{2}\right)^2+64 \left(x-\frac{1}{2}\right)^3+ O\left(\left(x-\frac{1}{2}\right)^4\right)$$

Answer 2

Hopefully, this is right!

Note that from the weighted AM-GM inequality, We have that $$h(x)=\log_2{\frac{1}{x^x(1-x)^{1-x}}} \ge \log_2\frac{1}{x^2+(1-x)^2}$$ Thus we have to show $$\left(1-\frac{x}{1-x}\right)^2 \ge 1-\log_2\frac{1}{2x^2-2x+1}=\log_2{(4x^2-4x+2)}$$ Substitute $x=\frac{a+1}{a+2}$, and we have $$f(a)=a^2 -\log_2\left(\frac{a^2}{(a+2)^2}+1 \right) \ge 0$$ For $a \ge -1$. Differentiating gives $$f'(a)=2a\left(1-\frac{1}{(a+2) (a^2+2 a+2) \log(2)}\right)$$ and this $f'(a)>0$ for $a>0$ alternatively $f(a) \ge f(0)=0$ for $a \ge 0$.

Also, notice the local maxima lies between $-1$ and $0$. But since $f(-1)=f(0)=0$, we have that $f(a) \ge 0$ for $-1 \le a \le 0$.

Our proof is done.

Answer 3

$$h(x) = x \log_2\frac{1}{x}+(1-x) \log_2\frac{1}{1-x}\ge1- \left(1-\frac{x}{1-x}\right)^2$$

If we let $x=\frac{1+y}{2}$ and push through the algebra, the claim is equivalent to:

$$1-\frac{1}{2}\log_2(1-y^2)-\frac{y}{2}\log_2\left(\frac{1+y}{1-y}\right)\ge1-\frac{4y^2}{(1-y)^2}$$

which can be rearranged to:

$$\frac{8y^2}{(1-y)^2}\ge \log_2(1-y^2) + y\log_2\left(\frac{1+y}{1-y}\right)$$

Now, using the well-known $\ln u\le u-1$:

$$\ln v^2\le v^2-1\implies \ln v \le \frac{v^2-1}{2}$$

and taking $v=\frac{1+y}{1-y}$, this becomes:

$$\ln\left(\frac{1+y}{1-y}\right)\le \frac{2y}{(1-y)^2}$$

Noting that $\log_2(1-y^2)\le0$, we can see

$$\log_2(1-y^2) + y\log_2\left(\frac{1+y}{1-y}\right)\le y\frac{1}{\ln2}\frac{2y}{(1-y)^2}=\frac{2}{\ln2}\frac{y^2}{(1-y)^2}\le \frac{8y^2}{(1-y)^2}$$

and we are done for $y>0$.

For $y<0$ it's a little trickier, because the other $\log$ term does come into play - still working out a nice argument for how to bound things appropriately.

Answer 4

Here is a definite integral approach.

Using the known identity (for all $u > -1$) $$\ln (1 + u) = \int_0^\infty \frac{1 - \mathrm{e}^{-us}}{s}\mathrm{e}^{-s}\,\mathrm{d} s, \tag{1}$$ we have \begin{align*} &-\frac{x\ln x}{\ln 2} - \frac{(1 - x)\ln (1 - x)}{\ln 2} \\ =\,& \int_0^\infty \left[x(\mathrm{e}^{s(1 - x)} - 1) + (1 - x)(\mathrm{e}^{sx} - 1)\right]\frac{\mathrm{e}^{-s}}{s\ln 2}\,\mathrm{d} s\\ =\,& \int_0^\infty x(1 - x)\left(\frac{\mathrm{e}^{s(1 - x)} - 1}{1 - x} + \frac{\mathrm{e}^{sx} - 1}{x}\right)\frac{\mathrm{e}^{-s}}{s\ln 2}\,\mathrm{d} s\\ =\,& \int_0^\infty x(1 - x)\left(\int_0^s (\mathrm{e}^{t(1-x)} + \mathrm{e}^{tx}) \,\mathrm{d} t\right)\frac{\mathrm{e}^{-s}}{s\ln 2}\,\mathrm{d} s \\ \ge\,& \int_0^\infty x(1 - x)\left(\int_0^s 2\sqrt{\mathrm{e}^{t(1-x)} \cdot \mathrm{e}^{tx}} \,\mathrm{d} t\right)\frac{\mathrm{e}^{-s}}{s\ln 2}\,\mathrm{d} s \\ =\,& \int_0^\infty x(1 - x)\left(\int_0^s 2\mathrm{e}^{t/2} \,\mathrm{d} t\right)\frac{\mathrm{e}^{-s}}{s\ln 2}\,\mathrm{d} s\\ =\,& \int_0^\infty x(1 - x)(4\mathrm{e}^{s/2} - 4)\frac{\mathrm{e}^{-s}}{s\ln 2}\,\mathrm{d} s\\ =\,& 4x(1 - x) \tag{2} \end{align*} where in (2) we have used $\ln (1 - 1/2) = \int_0^\infty \frac{1 - \mathrm{e}^{s/2}}{s}\mathrm{e}^{-s}\,\mathrm{d} s$ (simply letting $u = -1/2$ in (1)).

Also, we have $$4x(1 - x) - \left[1- \left(1-\frac{x}{1-x}\right)^2\right] = \frac{x(2 - x)(1 - 2x)^2}{(1 - x)^2} \ge 0.$$

We are done.

Answer 5

As noted in my comment, it suffices to show the inequality for $x\in[0,\frac{1}{2}]$. Note that the inequality becomes an equality at the endpoints, $0$ and $\frac{1}{2}$. The inequality is tighter around $\frac{1}{2}$ than around $0$. In our proof, we will distinguish two (overlapping) cases, $x$ near $0$ or $x$ near $\frac{1}{2}$. When $x$ is near $\frac{1}{2}$, we Taylor-expand the logs at $\frac{1}{2}$. When $x$ is near $0$, we use cruder (constant, in fact) bounds on the logs.

We have to show that

$$ x\log(x)+(1-x)\log(1-x) \leq \log(2)\left(\frac{3x^2-2x}{(1-x)^2}\right) \tag{1} $$

As $\frac{\log(1-x)-\log(\frac{1}{2})}{\frac{1}{2}-x}\leq 2 \leq \frac{\log(\frac{1}{2})-\log(x)}{\frac{1}{2}-x}$, we have $\log(x) \leq (-1-\log(2))+2x$ and $\log(1-x) \leq (1-\log(2))-2x$, so (1) will be true whenever

$$ x\left[(-1-\log(2))+2x\right]+(1-x)\left[(1-\log(2))+2x\right] \leq \log(2)\left(\frac{3x^2-2x}{(1-x)^2}\right) \tag{2} $$

By construction, (2) is simplifiable by $(x-\frac{1}{2})^2$ and a little cleanup massaging shows that (2) is equivalent to $(1-x)^2 \leq \log(2)$. This shows (1) for $x\geq 1-\sqrt{\log(2)}$. Note that the number $1-\sqrt{\log(2)} \approx 0.167$ is strictly less than $0.2$.

Now, let us deal with the case when $x\leq 0.2$. Then $\log(x)\leq\log(0.2)$ and $\log(1-x)\leq 0$, so that it (1) is true whenever $$ x\log(0.2) \leq \log(2)\left(\frac{3x^2-2x}{(1-x)^2}\right) \tag{3} $$

Clearly, (3) is equivalent to $$ \frac{\log(0.2)}{\log(2)} \leq \frac{3x-2}{(1-x)^2} $$ Now, the RHS can be rewritten $-\frac{35}{16}+\frac{35(\frac{1}{5}-x)(\frac{3}{7}-x)}{16(1-x)^2}$ and we conclude the proof by noting that $\frac{\log(0.2)}{\log(2)} < -\frac{35}{16}$ because $\frac{\log(0.2)}{\log(2)} \approx -2.32$ and $-\frac{35}{16} \approx -2.18$.

Answer 6

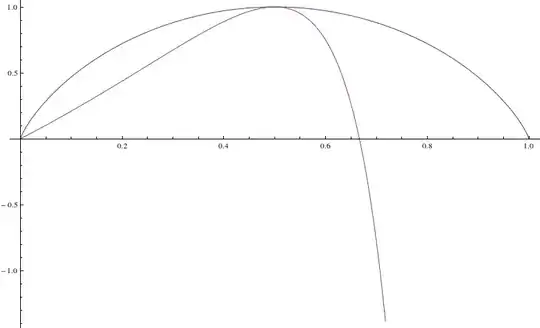
The long and painful way: "differentiating, and differentiating."

Define $f,g\colon (0,1)\to \mathbb{R}$ by $f(x) = 1-4\left(x-\frac{1}{2}\right)^2$ and $g(x) = 1-\left(1-\frac{x}{1-x}\right)^2$. We will show $$ h(x) \geq f(x) \geq g(x), \qquad x\in(0,1). $$

---

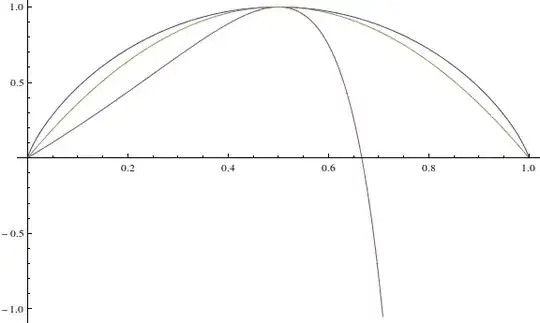
Claim. $h(x) \geq f(x)$ for all $x\in(0,1)$.

Proof. Both functions are $C^\infty$, and we have $$ h''(x) - f''(x) = \frac{-8}{x(1-x)} \left(x^2-x+\frac{1}{8\ln 2}\right) $$ which cancels at $x_0 \stackrel{\rm def}{=} \frac{1-\sqrt{1-\frac{1}{2\ln 2}}}{2}\simeq 0.236$ and $x_1 = 1-x_0$.

We thus have the following, as $\lim_{0^+} (h''-f'') = \lim_{1^-} (h''-f'') = -\infty$: $$ \begin{array}{|c|ccc|} \hline x & 0 & &x_0 & \frac{1}{2} & x_1 && 1 \\ \hline h''-f'' & -\infty &-&0&+&0& - &-\infty\\ \hline \end{array} $$

Moreover, since $h'(x) - f'(x) = \frac{1}{\ln 2}\left(8\ln 2 \cdot x + \ln\frac{1-x}{x} - 4\ln 2 \right)$, we have $\lim_{0^+} (h'-f') = - \lim_{1^-} (h'-f') = \infty$ and $(h'-f')(\frac{1}{2})=0$. Since $x_0 < \frac{1}{4}$ and $(h'-f')(\frac{1}{4}) = \frac{\ln\frac{3}{4}}{\ln 2} < 0$, we know that $(h'-f')(x_0) = -(h'-f')(x_1) < 0$.

$$ \begin{array}{|c|ccc|} \hline x & 0 & &x_0 && \frac{1}{2} && x_1 && 1 \\ \hline h''-f'' & -\infty &-&0&&+&&0& - &-\infty\\ \hline h'-f' & +\infty &\searrow&-&\nearrow& 0&\nearrow&+& \searrow &-\infty\\ \hline \end{array} $$ This in turn implies that $h'-f'$ has exactly three roots, namely $r_0 < \frac{1}{2} < r_1$ with $r_1 = 1-r_0 \in (0,x_0)$.

$$ \begin{array}{|c|ccc|} \hline x & 0 & &r_0 && \frac{1}{2} && r_1 && 1 \\ \hline h'-f' &&+&0&-& 0&+&0& - &\\ \hline h-f &0&\nearrow&&\searrow& 0&\nearrow&& \searrow 0&\\ \hline \end{array} $$ This implies the claim, as $\lim_{0^+}(h-f) = (h-f)(1/2) = \lim_{1^-}(h-f) =0$: $h\geq f$ on $(0.1)$.

---

Claim. $f(x) \geq g(x)$ for all $x\in(0,1)$.

Proof. Writing out the expression and massaging it, we get that for all $x\in (0,1)$ $$ f(x) - g(x) = \frac{x (2-x) (1-2 x)^2}{(1-x)^2}\geq 0.$$

Answer 7

The Hermite interpolation polynomial for the function $h(x)$ at points $0$, $\frac{1}{2}$,$\frac{1}{2}$ $1$ is $P(x)= 4 x(1-x)$. The remainder formula is $$f(x) - P(x) = \frac{f^{(4)}(\xi_x)x(x-\frac{1}{2})^2 (x-1)}{4!}$$ where $\xi_x$ is an intermediate point between $0$, $\frac{1}{2}$, $1$ and $x$ ( inside their convex hull). Now we only need to that on $(0,1)$ the fourth derivative of $f$ is negative. Indeed, we have $$f^{(4)}(x) = -\frac{2}{\log 2}\left (\frac{1}{x^3} + \frac{1}{(1-x)^3} \right)$$ We conclude that for $x\in (0,1)$, $x\ne \frac{1}{2}$ we have $$h(x) > 4 x(1-x)$$

Now it is enough to check that for $x\in (0,1)$, $x\ne \frac{1}{2}$ we have $$4x(1-x) > 1- (1- \frac{x}{1-x})^2$$ Indeed, their difference equals $\frac{x(2-x)(2x-1)^2}{(1-x)^2}>0$.

Note: this stronger inequality we proved is mentioned in the Wikipedia article on binary entropy function that was quoted by the OP. Worth thinking about the higher estimate.

$\bf{Added:}$ Using the Taylor expansion at $x=\frac{1}{2}$ we get $$h(x) = 1 - \frac{2}{\log 2} (x-\frac{1}{2})^2 - c_4 (x-\frac{1}{2})^2 - \cdots $$ while $$4x(1-x) = 1 - 4 (x-\frac{1}{2})^2$$ So we can see the inequality from the Taylor series expansion. Moreover, we can get an exponent $\alpha$ so that $$4x(1-x)^{\alpha} -h(x)$$ has a zero second derivative. $\alpha$ is such that $\alpha \cdot 4 = \frac{2}{\log 2}$, that is, $\alpha = \frac{1}{\log 4}$. It is not hard to check that all the coefficients of the Taylor expansion of $$(4x(1-x))^{\frac{1}{\log 4}}- h(x)$$ are positive, and so we get the upper estimate mentioned in Wikipedia.

The plots of the functions $4x(1-x)$, $h(x)$, $(4x(1-x))^{\frac{1}{\log 4}}$.

$\bf{Added:}$ Numerics suggest that we have the stronger inequality $(4x(1-x))^{0.9}< h(x)$ on $(0,1)$, $x\ne \frac{1}{2}$. Note that $\frac{1}{\log 4} = 0.721\ldots$.

$\bf{Added:}$ Using the Hermite interpolation polynomial for $h(x)$ at points $0, \frac{1}{2} ^{(4)}, 1$ we can show that (for $x\ne \frac{1}{2}$) $$h(x) > 4x(1-x)(1 + k( 2 x-1)^2)$$ for $k = 1-\frac{1}{\log 4} = 0.27865\ldots$. We can also take $k =0.25=\frac{1}{4}$ getting the simpler lower estimate $$h(x) > 4x(1-x)(1+ (x-\frac{1}{2})^2)$$

For the upper estimate we can not use a polynomial, because $h$ has at $1_{-}$ derivative $-\infty$.

Answer 8

This is a slight economization of the elegant answer of @River Li. $$\ln(1+u)= u\int_0^1 dt\frac1{1+ut}=u\int_0^1 dt \int_0^\infty \mathrm ds\, e^{-(1+ut)s}.$$ Applying the above double integral representation thrice and obtain \begin{align} &-x\ln x- (1 - x)\ln (1 - x) \\ =\,& x(1-x)\int_0^1dt\int_0^\infty ds\, e^{-s} \,(e^{(1-x)st}+e^{xst}) \\ \ge\,& 2x(1-x)\int_0^1dt\int_0^\infty ds\, e^{-s} \,e^{\frac{st}2} \\ =\,& 4x(1-x)\ln 2. \end{align} We finish the proof with the last step in @River Li's answer.

Answer 9

Hint : $$\frac{1}{\ln\left(2\right)}\left(x\ln\left(\frac{1}{x}\right)+\left(1-x\right)\ln\left(\frac{1}{1-x}\right)\right)\geq f(x)=-\frac{\ln\left(1-2\left(1-x\right)x\right)}{\ln\left(2\right)}\geq 1-\left(1-\frac{x}{1-x}\right)^{2}$$

Use second derivative and difference .

Some details :

We have the easy inequalities $x\in(2/3,1)$:

$$1-\left(1-\frac{x}{1-x}\right)^{2}\leq 16\left(1-x\right)^{2}x^{2}\leq -\frac{\ln\left(1-2\left(1-x\right)x\right)}{\ln2}$$

$$\left(2x-2\right)\ln\left(1-2\left(1-x\right)x\right)\leq \ln\left(\frac{1}{x}\right)$$

$$-2\left(x-\frac{1}{2}\right)\ln\left(1-2\left(1-x\right)x\right)\leq \left(1-x\right)\left(-\ln\left(\frac{1}{x}\right)+\ln\left(\frac{1}{1-x}\right)\right)$$

We have on $x\in[0.5,2/3]$ $a=\frac{4}{\ln 2}$:

$$a\left(-x^{2}+\frac{3}{2}x-\frac{1}{2}-\frac{1}{a}\right)\ln\left(1-2\left(\left(1-x\right)x\right)\right)\leq \ln\left(\frac{1}{x}\right)$$

$$a\left(x-\frac{1}{2}\right)\left(x-1\right)\ln\left(1-2\left(\left(1-x\right)x\right)\right)-\left(1-x\right)\left(\ln\left(\frac{1}{1-x}\right)+\ln\left(x\right)\right)\leq 0$$

And on $x\in(0.5,0.75)$ :

$$16\left(1-x\right)^{2}x^{2}>1-\left(1-\frac{1-x}{x}\right)^{2}$$

I recognize it's not very elegant but it could be useful I think somewhere .