3

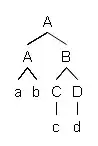
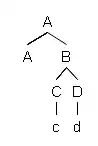
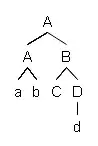
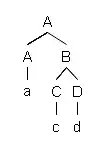
Let $T=(V,E)$ be a directed rooted tree with root $r \in V$. A root subtree$^1$ of $T$ is a directed rooted tree $T'=(V',E')$ that fulfills the following conditions:

  • $T'$ is a subgraph of $T$,
  • $r \in V'$
  • for each node $v \in V'$, either all children of $v$ in $T$ are also in $V'$, or none of them is.

For example, let

$T=$ $T'=$ $T''=$ $T'''=$ .

Then both $T'$ and $T''$ are root subtrees of $T$, but $T'''$ isn't.

Now my question is this: How can the maximum number of root subgraphs of a tree T be expressed as a function of its size $s$?

More formally, I'm looking for a closed-form expression for the function $f$ s.t. $f(s) = \max\{n \in \mathbb{N} \mid \text{there is a tree $T$ with size $s$ s.t. $T$ has $n$ root subtrees } \}$. I'm assuming $f = \mathcal{O}(2^s)$, but I'm interested in the exact number.

Edit: If this helps, I think that the first values of $f$ are:

  • $f(s) = s$, $1 \leq s \leq 5$
  • $f(6) = 7$
  • $f(7) = 9$

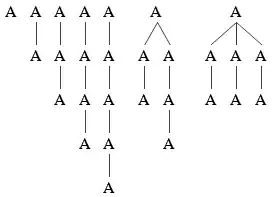
If I am correct, then examples for trees of size $1, \ldots, 7$ that have the maximum number of root subtrees are:

$^1$ I made that name up as I don't know whether there already is a name for this concept.

vauge
  • 323

1 Answers1

1

The number of rooted subtrees of a tree is the product of the numbers of rooted subtrees of the root's children plus one. Here's code that recursively computes $f(s)$. The result is OEIS sequence A007601, which is a shifted version of OEIS sequence A000792. Apparently for $s\ge3$ we have

$$ f(s)=1+\left(\left\{\frac s3\right\}+\frac23\right)3^{\left\lfloor\frac s3\right\rfloor}\;, $$

where $\{x\}$ denotes $\lfloor x\rfloor-x$, the fractional part of $x$.

Note that you got $f(7)$ wrong; $f(7)=10$, since it's better to have two children with $3$ nodes each than three children with $2$ nodes each.

joriki
  • 238,052