$a,b,c >0$, prove $\sqrt[2]{\frac{a}{b+c}}+\sqrt[3]{\frac{b}{c+a}}+\sqrt[4]{\frac{c}{a+b}} \geqslant \frac{7}{12} \cdot2^{\frac67} \cdot 3^{\frac47}$

Question

$a,b,c >0$, prove $$\sqrt[2]{\frac{a}{b+c}}+\sqrt[3]{\frac{b}{c+a}}+\sqrt[4]{\frac{c}{a+b}} \geqslant \frac{7}{12} \cdot2^{\frac67} \cdot 3^{\frac47}$$

What I tried:
1) It seems like a Nesbitt inequality. But I tried to imitate some Nesbitt proofs but was not successful.
2) Update: Following Frank's suggestion: the inequality is homogeneous, and can assume $a+b+c=1$ to reduce variables.
3) Test on Excel a lot of pairs $(a,b,c)$ and convinced myself the inequality is true and can be achievable.
4) Try Bernoulli's inequality but failed miserably.

---

Edit by Andreas, 2018-06-15: Sorry, but this is a wrong claim (counterexamples can be -and were - given), however it is a very interesting task. What should really be proved is $$\sqrt[2]{\frac{a}{b+c}}+\sqrt[3]{\frac{b}{c+a}}+\sqrt[4]{\frac{c}{a+b}} \geqslant 3 \cdot (\frac12)^{\frac23}$$ where the RHS is lower than the claimed $\frac{7}{12} \cdot2^{\frac67} \cdot 3^{\frac47}$, and the RHS is tight, i.e. values of $(a,b,c)$ can be given such that the RHS is indeed an infimum.

Answer 1

This is not an answer. Just sharing a possible way to simplify the problem.

From the new answers/comments it is clear that the original bound is wrong, and so, this post should be taken as a failed attempt, though the method might be useful, and so I will leave this intact.

Let's introduce new variables:

$$\frac{c}{a+b}=u$$

$$\frac{b}{c+a}=v$$

Then, we can show that:

$$\frac{a}{b+c}=\frac{1-uv}{u+v+2uv}$$

Now the inequality becomes:

$$u^{1/4}+v^{1/3}+\sqrt{\frac{1-uv}{u+v+2uv}} \geq \frac{7}{12} \cdot2^{\frac67} \cdot 3^{\frac47}$$

For $a,b,c>0$ we always have $uv \leq 1$.

---

I had a lucky guess (which remains to be proven), that the minimum of the function:

$$f(u,v)=u^{1/4}+v^{1/3}+\sqrt{\frac{1-uv}{u+v+2uv}}$$

is the same as the miminum of the following two functions:

$$f(u,1/u), \qquad f(1/v,v)$$

Which is confirmed by Mathematica output:

Note that this is the same as $uv=1$, which makes the third term exactly zero.

Minimization leads to the following for the first case:

$$u=\left(\frac{4}{3}\right)^{12/7}, \qquad v= \left(\frac{3}{4}\right)^{12/7}$$

Which makes the function:

$$f_{\text{min}}=\left(\frac{4}{3}\right)^{3/7}+\left(\frac{3}{4}\right)^{4/7}=\left(\frac{3}{4}\right)^{4/7} \left(1+\frac{4}{3} \right)=\frac{7}{12} \cdot2^{\frac67} \cdot 3^{\frac47} $$

Answer 2

A solution will be given by first showing that two of the arguments of the roots are always less than 1, and that for any fixed sum $s = a+b$ (or of any other two variables), the minimum of the LHS is obtained if one variable is taken to be zero. After that, the LHS can be minimized.

It shows (following the comment by fedja) that $\underline{\rm{the \; OP's \;claim \;is \;actually \;false.}}$ A correct lower bound will be given which is $3 \cdot (1/2)^{2/3} \simeq 1.8899$.

Let us give names to the three arguments of the roots: $$f = \frac{a}{b+c}\\ g = \frac{b}{c+a} \\ h = \frac{c}{a+b} $$ Observe that the sum expression is homogenous in $(a,b,c)$. So we can demand $a+b+c=6$.
(The number 6 was taken to avoid fractions later on.)

This gives for the three arguments: $$f(a) = -1 +\frac{6}{6-a}\\ g(b) = -1 +\frac{6}{6-b}\\ h(c) = -1 +\frac{6}{6-c}\\ $$ Any argument function rises with its variable, i.e. $f(a)$ rises with $a$ etc.

All three argument functions are equal ($= 1/2$) for $a=b=c=2$. The argument functions obtain the value $f=1$ for $a=3$, etc. This means that we will always have 2 or 3 argument functions which are less than 1. For if we had at least two argument functions which are greater than 1, we would have $a+b >6$ which is a contradiction.

From the discussion above, for any given $(a,b,c)$, let us choose the two argument functions (for the sake of the discussion, say, $f$ and $g$)) which have the smallest values (which are less than 1). Then we have $a+b = s \le 4$. For if $s >4$, these were not the two argument functions which have the smallest values, as $c <2$.

Now for any fixed $s\le 4$, we have that $\sqrt{f(a)}+\sqrt[3]{g(s-a)}$ takes the smallest value (infimum) at the boundary, i.e. either at $a=0$ or $a = s$, i.e. $b=0$ (likewise for a pair of other roots). It takes a lengthy discussion on values and derivatives to show this. Notably, the statement is false for some $s>4$.

The following picture illustrates the situation for $s = 3$ (lower curve) and $s = 4$ (upper curve):

This means that, for a lower limit, one variable out of $(a,b,c)$ will be zero, and the corresponding root will be zero. All the dicussions above did not specify yet which one. So we are left with the three cases of choosing that variable.

When taking $a=0$, one obtains: $$ \sqrt[2]{\frac{a}{b+c}}+\sqrt[3]{\frac{b}{c+a}}+\sqrt[4]{\frac{c}{a+b}} \\ \geqslant \sqrt[3]{\frac{b}{c}}+\sqrt[4]{\frac{c}{b}} = x^{1/3} + x^{-1/4} $$

where we introduced $x = \frac{b}{c}$. It is now easy to find the minimum w.r.t. $x$, resulting in $x = (3/4)^{12/7}$. So

$$ \sqrt[2]{\frac{a}{b+c}}+\sqrt[3]{\frac{b}{c+a}}+\sqrt[4]{\frac{c}{a+b}} \\ \geqslant \left(\frac{4}{3}\right)^{3/7}+\left(\frac{3}{4}\right)^{4/7}=\left(\frac{3}{4}\right)^{4/7} \left(1+\frac{4}{3} \right)=\frac{7}{12} \cdot2^{\frac67} \cdot 3^{\frac47} \simeq 1.9796 $$

which is the lower bound conjectured by the OP. However, this is not the best option. As indicated by fedja, taking $b=0$ will give a lower bound (which, again, cannot be improved by taking $c=0$). fedja may post his own solution on that, I do not want to steal it. The lower bound (infimum) is then, with the same method as described above, $3 \cdot (1/2)^{2/3} \simeq 1.8899$. This is obtained when $a = c \cdot (1/2)^{4/3}$.

As a "fun fact", compare this to the Nesbitt limit which is obtained for $a=b=c$. The LHS value is then $\sqrt[2]{\frac12}+\sqrt[3]{\frac12}+\sqrt[4]{\frac12} \simeq 2.3417$ so this is far from the true minimum.

This completes the proof. $\quad \quad \Box$

Answer 3

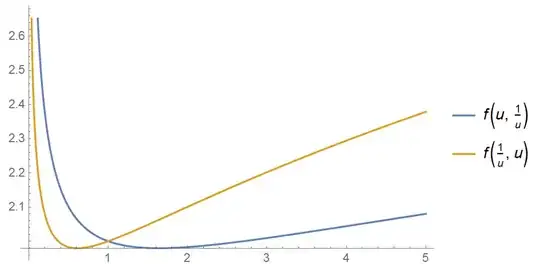
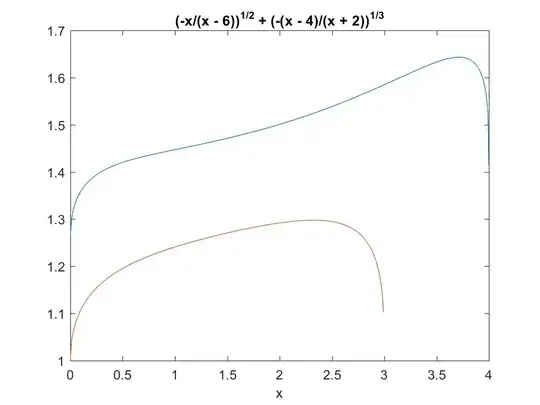
The task transformation.

The task is homogenius by $a, b, c.$

Let WLOG $$a+b+c = 1,\quad (a,b.c)\in\mathbb R_+^3,$$ $$x=\sqrt[2]{\dfrac{a}{1-a}},\quad y=\sqrt[3]{\dfrac{b}{1-b}},\quad z=\sqrt[4]{\dfrac{c}{1-c}},$$ then the equivalent task is to prove the inequality $$f(x,y,z) = x+y+z\ge \dfrac7{12}\cdot2^{6/7}\cdot3^{4/7}\tag1$$ under constraints $$\dfrac1{1+x^2} + \dfrac1{1+y^3} + \dfrac1{1+z^4} = 2,\quad (x,y,z)\in\mathbb R_+.\tag2$$ The least value of $f(x,y,z)$ can be achieved on the edges of the given area or in the stationary points.

---

Checking of the edges.

$$\underline{\mathrm{Case\ x\to 0.}}$$ $$\dfrac1{1+y^3} + \dfrac1{1+z^4} = 1,\quad \dfrac1{1+z^4} = \dfrac{y^3}{1+y^3},$$ $$\dfrac1{1+z^4} = \dfrac1{1+y^{-3}} ,\quad z=y^{-3/4},$$ then the least value of $$f_1(y) = y+y^{-3/4}$$ achieves when $$f_1'(y) = 1-\dfrac34x^{-7/4} = 0,\quad y_{1m} = \left(\dfrac34\right)^{4/7},$$ and equals to $$f_{1m} = \dfrac7{12}2^{6/7}3^{4/7}\approx1.979626\tag3$$ (see also Wolfram Alpha)

$$\underline{\mathrm{Case\ y\to 0.}}$$

$$\dfrac1{1+x^2} + \dfrac1{1+z^4} = 1,\quad \dfrac1{1+x^2} = \dfrac{z^4}{1+z^4},$$ $$\dfrac1{1+x^2} = \dfrac1{1+z^{-4}},\quad x=\dfrac1{z^2},$$ then the least value of $$f_2(z) = z+\dfrac1{z^2}$$ achieves when $$f_2'(z) = 1-2z^{-3} = 0,\quad z_{2m} = \sqrt[3]2,$$ and equals to $$f_{2m} = \dfrac32 2^{1/3}\approx 1.889882\tag4$$ (see also Wolfram Alpha).

This means that $$x_{2m} = \dfrac1{\sqrt[3]4},\quad \dfrac{a}{1-a} = \dfrac1{2\sqrt[3]2},\quad a=\dfrac1{2\sqrt[3]3+1},$$ $$z_{2m} = \sqrt[3]2,\quad \dfrac{c}{1-c} = 2\sqrt[3]2, \quad c=\dfrac{2\sqrt[3]3}{2\sqrt[3]3+1}.$$

Easy to check that for $$a=\dfrac1{2\sqrt[3]3+1}, \quad c=\dfrac{2\sqrt[3]3}{2\sqrt[3]3+1},$$ $$\sqrt[2]{\dfrac a{1-a}} + \sqrt[4]{\dfrac{c}{1-c}} = f_{2m} \le f_{1m}$$

$$\underline{\mathrm{Case\ z\to 0.}}$$ $$\dfrac1{1+x^2} + \dfrac1{1+y^3} = 1,\quad \dfrac1{1+x^2} = \dfrac{y^3}{1+y^3},$$ $$\dfrac1{1+x^2} = \dfrac1{1+y^{-3}},\quad x=y^{-3/2},$$ then the least value of $$f_3(y) = y+y^{-3/2}$$ achieves when $$f_3'(y) = 1-\dfrac32y^{-5/2} = 0,\quad y_{3m} = \left(\dfrac32\right)^{2/5},$$ and equals to $$f_{3m} = \dfrac562^{3/5}3^{2/5}\approx1.960132\tag5$$ (see also Wolfram Alpha).

---

The stationary points

The stationary points of $f(x,y,z)$ can be defined using Lagrange multipliers method, as the stationary points of the function $$F(x,y,z,\lambda)= x+y+z + \lambda\left(\dfrac1{1+x^2} + \dfrac1{1+y^3} + \dfrac1{1+z^4}-2\right),$$ from the system $$F'_x = F'_y = F'_z = F'_\lambda = 0,$$ or \begin{cases} 1-\lambda\dfrac{2x}{(1+x^2)^2}=0\\[4pt] 1-\lambda\dfrac{3y^2}{(1+y^3)^2}=0\\[4pt] 1-\lambda\dfrac{4z^3}{(1+z^4)^2}=0\\[4pt] \dfrac1{1+x^2} + \dfrac1{1+y^3} + \dfrac1{1+z^4} = 2\\[4pt] (x,y,z)\in\mathbb R_+, \end{cases} \begin{cases} &\dfrac{1+y^3}{\sqrt3y} = \dfrac{1+x^2}{\sqrt{2x}} = \dfrac{1+z^4}{2z\sqrt z},\\[4pt] &\dfrac1{1+y^3} = \dfrac{x^2}{1+x^2} + \dfrac{z^4}{1+z^4}\\[4pt] &(x,y,z)\in\mathbb R_+,\\[4pt] \end{cases} $$\dfrac1{\sqrt3 y} = \dfrac{x\sqrt{2x}}2+\dfrac{z^2\sqrt z}2.$$ Let $$s=\sqrt{2x},\quad t = \sqrt z,\tag6$$ then $$y = \dfrac4{\sqrt3(s^3+2t^5)},\tag7$$ $$\dfrac{s^3+2t^5}4 + \dfrac{16}{9}\dfrac{\sqrt3}{(s^3+2t^5)^2} = \dfrac{s^4+4}{4s}=\dfrac{t^8+1}{2t^3}$$

\begin{cases} t^3(s^4+4)=2(t^8+1)s\\[4pt] t^5s - 2 + \dfrac{32}{3\sqrt3}\dfrac{s}{(s^3+2t^5)^2} = 0 \end{cases}

\begin{cases} 2ts\cdot t^8 - 4t^4 + 2ts-(ts)^4=0\\[4pt] 3\sqrt3(t^5s - 2)(s^3+2t^5)^2+32s=0, \end{cases} Let $$p=ts,\tag8$$ then \begin{cases} 2pt^8 - 4t^4 + 2p-p^4=0\\[4pt] 3\sqrt3(pt^4 - 2)(p^3+2t^8)^2+32pt^5=0,\tag9 \end{cases} with the positive solutions $$\binom{p}{t}\in\left\{\binom{1.03999}{1.13498}, \binom{0.87867}{0.764489}\right\},$$ $$\begin{pmatrix}x\\y\\z\end{pmatrix}\in \left\{\begin{pmatrix}0.419809\\0.509112\\1.28818\end{pmatrix}, \begin{pmatrix}0.66051\\1.13174\\0.584443\end{pmatrix}\right\},$$ $$\begin{pmatrix}a\\b\\c\\f\end{pmatrix}\in \left\{\begin{pmatrix}0.149833\\0.116576\\0.733591\\2.217101\end{pmatrix}, \begin{pmatrix}0.303754\\0.591766\\0.104482\\2.376693\end{pmatrix}\right\},$$

---

Results

1. The issue inequality is wrong, because for $$a=\dfrac1{2\sqrt[3]3+1},\quad b\to 0,\quad c=\dfrac{2\sqrt[3]3}{2\sqrt[3]3+1},$$ $$LHS = \dfrac32 2^{1/3} < \dfrac7{12}2^{6/7}3^{4/7}.$$

2. Proved that in the task constraints $$\sqrt[2]{\dfrac a{b+c}} + \sqrt[3]{\dfrac b{c+a}} + \sqrt[4]{\dfrac c{a+b}} \ge \dfrac32\cdot2^{1/3}\approx1.889882.$$

---

Appendium

\begin{cases} p^4 = 2p(t^8+1) - 4t^4\\[4pt] 3\sqrt3(pt^4 - 2)(p^4+2pt^8)^2+32p^3t^5=0, \end{cases}

\begin{cases} p^4 = 2p(t^8+1) - 4t^4\\[4pt] 3\sqrt3(pt^4 - 2)(2t^8p+p-2t^4)^2+8p^3t^5=0\tag{10} \end{cases}

Let $$t=q\sqrt3,$$ then system $(10)$ changes to the form \begin{cases} p^4 = 162pq^8 + 2p - 36q^4\\[4pt] (9pq^4 - 2)((p^4-162pq^8)^2+648p^5q^8)+96pq^5=0, \end{cases} and can be resolved using the polynomial reducing way.

Answer 4

It's wrong. Try $a=0.63^2$, $c=1$ and $b\rightarrow0^+$.