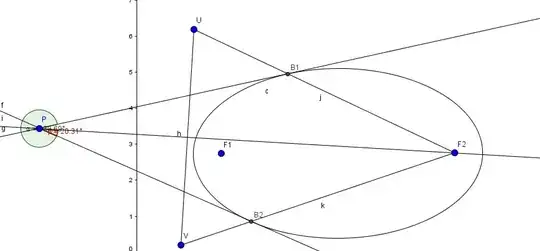
first please take a loot at this:
Given is an ellipse with foci $F1, F2$ and an external point $P$. Through P I have constructed two tangents to the ellipse.
I need to show that: $\angle F1PB1 = \angle B2PF2 $ and $\angle B1F2P = \angle PF2B2$. (ignore the angles around P, they are not meant to be seen here). This is what I tried so far:
- (For the second part I could show that $PF2$ is the bisectrix of $\angle UF2V$.)
- $U$ and $V$ can be created by reflecting $F1$ at $|PB1| and |PB2|$.
- Therefore I have $F1B1 = UB1$ and $F1B2 = VB2$ as well as $UP = F1P = VP$.
Any ideas, how to proof it?