21

$x,y,z >0$ and $x+y+z=3$, prove $$\tag{1}\frac{xy}{5y^3+4}+\frac{yz}{5z^3+4}+\frac{zx}{5x^3+4} \leqslant \frac13$$

My first attempt is to use Jensen's inequality. Hence I consider the function $$f(x) =\frac{x}{5x^3+4}$$ Compute second derivative we have $$\tag{2}f''(x)=\frac{30x^2(5x^3-8)}{(5x^3+4)^3}$$

$(2)$ shows that the function is neither concave or convex. So I don't think Jensen useful here.

The author of $(1)$ is the same as of this inequality.

River Li
  • 37,323
HN_NH
  • 4,361
  • It may be useful to notice that $\frac{x}{4}-f(x)$ is bounded by $\frac{135 x}{556}$ on $(0,3)$ or to exploit some algebraic trick like here: http://math.stackexchange.com/questions/1790541/show-that-frac-1-1-a-frac-1-1-b-frac-1-1-c-ge-frac/1790574#1790574 – Jack D'Aurizio May 31 '16 at 01:33
  • Since in this case the only stationary point seems to be $(1,1,1)$, it is worth trying to switch to the homogeneous inequality, clear denominators and apply Muirhead and Schur's inequality. Kind of tedious, however. – Jack D'Aurizio May 31 '16 at 01:49
  • @HN_NH Kind of irrelvant, but would you be able to recommend where did you start learning inequalities or any books you would recommend? – bigfocalchord Jun 01 '16 at 12:05
  • My dad is a university professor. I was trained on solving inequality by him. The main textbook my dad preferred is "Inequality" by Hardy and Polya. Currently I am self learning math. – HN_NH Jun 01 '16 at 22:21
  • 2
    Function $f(x)=\frac{x}{5x^3+4}$ happens to have a maximum ( https://www.wolframalpha.com/input/?i=x%2F(4%2B5%20x%5E3)) at $x=\sqrt[3]{\frac{2}{5}}$. Thus $$f(x) \leq \frac{1}{6}\cdot \sqrt[3]{\frac{2}{5}}$$ As a result $$\frac{xy}{5y^3+4} + \frac{yz}{5z^3+4} + \frac{zx}{5x^3+4}=xf(y)+yf(z)+zf(x) \leq \frac{1}{6}\cdot \sqrt[3]{\frac{2}{5}}\cdot(x+y+z)=\frac{1}{2}\cdot \sqrt[3]{\frac{2}{5}}$$ which is $\approx 0.3684$, close to $0.333333...$ – rtybase Jun 21 '16 at 08:56
  • @rtybase: This comment IMHO has not received enough attention. Why didn't you convert it into an answer in the first place? I find it better than the rest of the analyticals I've seen here. (And BTW, you don't need a computer algebra package to determine such a simple derivative :-) – Han de Bruijn Jul 03 '16 at 18:25
  • @HandeBruijn: It's just an observation, not an answer, imo. – rtybase Jul 03 '16 at 19:52
  • New solution, it seems interesting. – Yuri Negometyanov Aug 05 '16 at 11:17

2 Answers2

7

We can use the BW ( http://www.artofproblemsolving.com/community/c6h522084 )

We need to prove that $$\frac{1}{27(x+y+z)}\geq\sum\limits_{cyc}\frac{xy}{135y^3+4(x+y+z)^3}$$

  1. $x\leq y\leq z$, $y=x+u$, $z=x+u+v$.

Hence, $$27(x+y+z)\prod\limits_{cyc}(135x^3+4(x+y+z)^3)\left(\frac{1}{27(x+y+z)}-\sum\limits_{cyc}\frac{xy}{135y^3+4(x+y+z)^3}\right)=$$ $$=708588(u^2+uv+v^2)x^7+19683(263u^3+462u^2v+177uv^2-11v^3)x^6+$$ $$+39366(413u^4+961u^3v+603u^2v^2+55uv^3+2v^4)x^5+$$ $$+10935(2534u^5+7253u^4v+7007u^3v^2+2650u^2v^3+496uv^4+67v^5)x^4+$$ $$+1215(22600u^6+77007u^5v+99132u^4v^2+61585u^3v^3+21201u^2v^4+4341uv^5+388v^6)x^3+$$ $$+243(64879u^7+257249u^6v+406614u^5v^2+334330u^4v^3+161315u^3v^4+48417u^2v^5+8572uv^6+692v^7)x^2+$$ $$+27(2u+v)(89479u^7+360224u^6v+570894u^5v^2+463900u^4v^3+221075u^3v^4+67872u^2v^5+12872uv^6+1172v^7)x+$$ $$4(2u+v)^3(18871u^6+67548u^5v+87702u^4v^2+51889u^3v^3+17808u^2v^4+4944uv^5+556v^6)\geq$$ $$\geq708588v^2x^7-19683\cdot11v^3x^6+39366\cdot2v^4x^5\geq0$$

  1. $x\leq z\le y$, $y=x+u+v$, $z=x+v$.

Hence, $$27(x+y+z)\prod\limits_{cyc}(135x^3+4(x+y+z)^3)\left(\frac{1}{27(x+y+z)}-\sum\limits_{cyc}\frac{xy}{135y^3+4(x+y+z)^3}\right)=$$ $$=708588(u^2+uv+v^2)x^7+19683(-11u^3+42u^2v+327uv^2+263v^3)x^6+$$ $$+39366(2u^4-80u^3v+198u^2v^2+691uv^3+413v^4)x^5+$$ $$+10935(67u^5-125u^4v+193u^3v^2+3335u^2v^3+5417uv^4+2534v^5)x^4+$$ $$+1215(388u^6+399u^5v+168u^4v^2+16873u^3v^3+54097u^2v^4+58593uv^5+22600v^6)x^3+$$ $$+243(692u^7+2092u^6v-588u^5v^2+15920u^4v^3+110770u^3v^4+225579u^2v^5+196904uv^6+64879v^7)x^2+$$ $$+27(u+2v)(1172u^7+4252u^6v-3408u^5v^2+1700u^4v^3+118975u^3v^4+288609u^2v^5+266129uv^6+89479v^7)x+$$ $$4(u+2v)^3(556u^6+1299u^5v-4062u^4v^2+859u^3v^3+33027u^2v^4+45678uv^5+18871v^6)\geq$$ $$\geq708588u^2x^7+19683(-11)u^3x^6+39366(-4)u^4x^5+10935\cdot60u^5x^4\geq0$$

Done!

Michael Rozenberg
  • 194,933
4

Better a numerical / graphical solution than having no answer at all, I suppose?
Conditions similar to $\;x+y+z=3\;$ often occur in these inequalities, explicitly or implicitly.
(We shall see an example of the latter as well, later) Such conditions always have a geometrical interpretation, with a triangle, as is shown below.

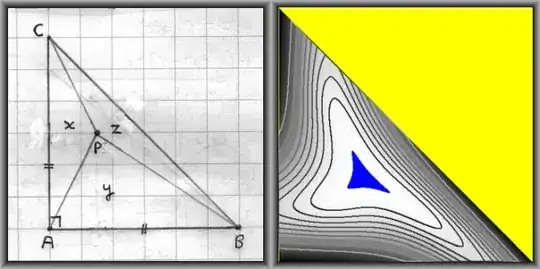
enter image description here

So-called area coordinates $(x,y,z)$ in the (rectangular & isosceles) triangle are defined as follows: $$ x/3 = \frac{\Delta APC}{\Delta ABC} \quad ; \quad y/3 = \frac{\Delta BPA}{\Delta ABC} \quad ; \quad z/3 = \frac{\Delta CPB}{\Delta ABC} $$ The $x$ and $y$ area-coordinates conform to the common Cartesian coordinates in this case, but the $z$ coordinate is different.

So far so good about the additional condition.
Solve $\,z\,$ therefrom and substitute the result $\,z=3-x-y\,$ into the inequality, giving: $$ f(x,y) = \frac{xy}{5y^3+4}+\frac{yz}{5z^3+4}+\frac{zx}{5x^3+4} \leqslant \frac13 $$ Not a formal proof is attempted again by plotting a contour map of the function, as depicted. Levels (nivo) of these isolines are defined (in Delphi Pascal) as:

nivo := min + sqrt(g/grens)*(max-min); { grens = 10 ; g = 1..grens }
The blackness of the isolines is proportional to the (positive) function values; they are almost white near the minimum and almost black near the maximum values. Maximum and minimum values of the function are observed to be: 

 4.87041188016219E-0003 < f < 3.33333101070422E-0001
And the maximum is observed to be near the triangle's center of gravity. The $\color{blue}{\mbox{blue}}$ spot is where $\,\left| f(x,y) - 1/3 \right| < 0.001$ .
The real maximum, of course, is at $\,(x,y,z) = (1,1,1)\,$ and it's value is $\,1/3$ .
Community
  • 1
Han de Bruijn
  • 17,070