Confusion in rotation matrix - rotation about $y$ axis

Question

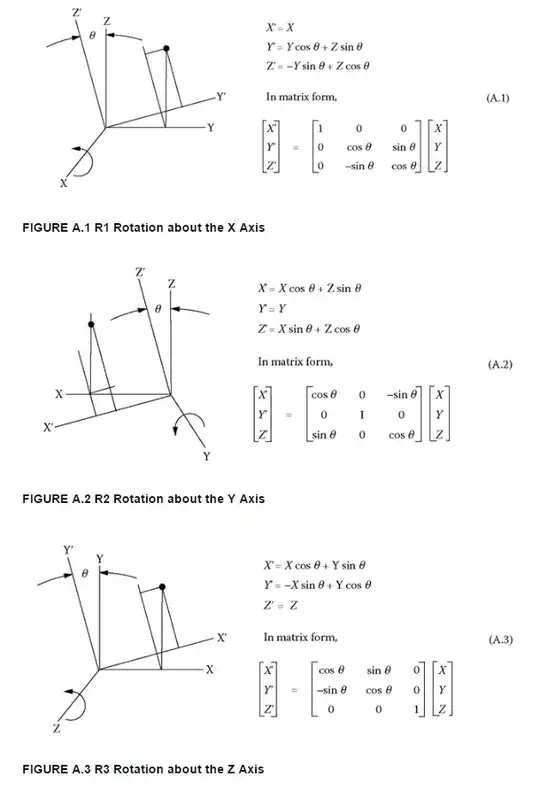
The rotation matrix about y axis should look like

$$\left[ \begin{array}{ccc} \cos\frac{\pi}{2} & 0 &\sin\frac{\pi}{2}\\ 0 & 1 & 0\\ -\sin\frac{\pi}{2} & 0 &\cos\frac{\pi}{2}\\ \end{array} \right] = \left[ \begin{array}{ccc} 0 & 0 &1\\ 0 & 1 & 0\\ -1& 0 &0\\ \end{array} \right] $$

Now, I pictured this rotation, and it should look like rotation about y axis, counterclockwise

I drew $(1,1,1)$ vector in original coordinate system, and in the new coordinate system, the vector should be $(-1,1,1)$

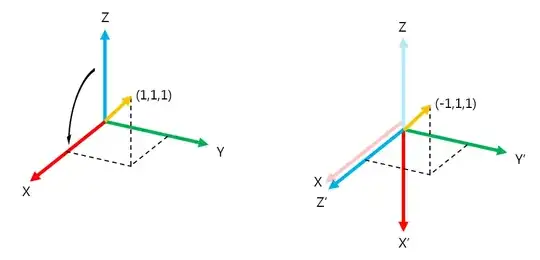
BUT! the matrix calculation gives otherwise.

$$ \left[ \begin{array}{ccc} 0 & 0 &1\\ 0 & 1 & 0\\ -1& 0 &0\\ \end{array} \right] \left[ \begin{array}{c} 1\\ 1\\ 1 \end{array} \right] =\left[ \begin{array}{c} 1\\ 1\\ -1 \end{array} \right] $$

Am I missing something?

Okay, it seems like I should rotate vector instead of coordinate system.

Then, How can you explain rotation about z axis?

The rotation matrix is $$ \left[ \begin{array}{ccc} \cos\frac{\pi}{2} &\sin\frac{\pi}{2} & 0\\ -\sin\frac{\pi}{2} &\cos\frac{\pi}{2} & 0\\ 0 & 0 & 1 \end{array} \right] = \left[ \begin{array}{ccc} 0 & 1 &0\\ -1 & 0 & 0\\ 0& 0 &1\\ \end{array} \right] $$

But... calculation is correct. $$ \left[ \begin{array}{ccc} 0 & 1 &0\\ -1 & 0 & 0\\ 0& 0 &1\\ \end{array} \right] \left[ \begin{array}{c} 1\\ 1\\ 1 \end{array} \right] =\left[ \begin{array}{c} 1\\ -1\\ 1 \end{array} \right] $$

IF you rotate the vector, then in the picture, it should be $(-1,1,1)$

Oh. god.... I think I am looking at the wrong source.

My book tells

well, clearly, googling gives me

http://what-when-how.com/the-3-d-global-spatial-data-model/rotation-matrix-derivation-the-3-d-global-spatial-data-model/

I think I solved my case. Thank you all.

the matrix is transforming the vector in the first space to another vector in the same space... — danimal, Jun 01 '16 at 15:42
How is it "what was previously the x-axis is now NEGATIVE z axis" ? not positive z axis? — user65452, Jun 01 '16 at 15:48
I don't understand why: "I drew (1,1,1) vector in original coordinate system, and in the new coordinate system, the vector should be (−1,1,1) ". In fact, the rotation matrix maps (1,1,1) to (1,1,-1). The matrix transform the vector. It doesn't express the old vector in the new basis. I think you are missing two different things — guestDiego, Jun 01 '16 at 15:48
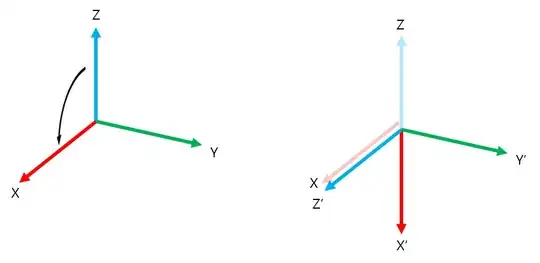
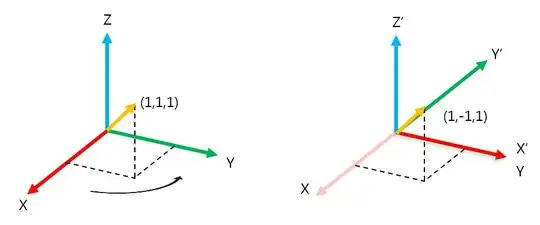
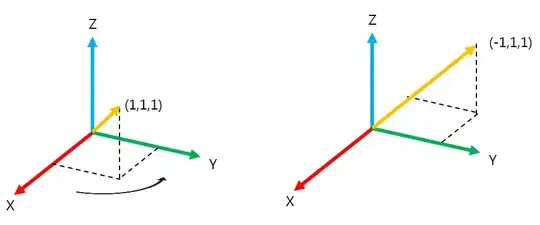
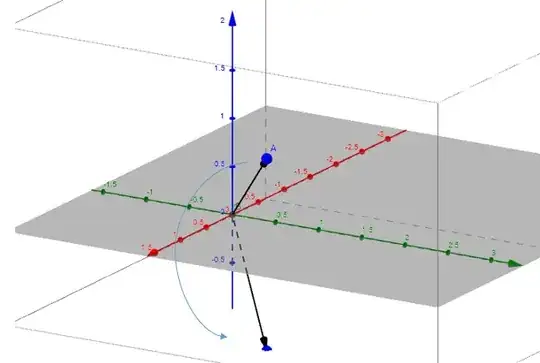
Initially, you wrote the matrix of a rotation of $\pi/2$ clockwise. — Bernard, Jun 01 '16 at 15:52
The book containing wrong notation is J. F. Rosenbaum, Bulk Acoustic Wave Theory and Devices (Artech House. Boston, 1988), — user65452, Jun 01 '16 at 16:50

Emilio Novati · Answer 1 · 2016-06-01T16:14:27.667

6

It seems that you are confusing active and passive rotations.

Your matrix $R$, applied to a vector $v$, give you a rotated vector $v'=Rv$ that is expressed in the same reference system than $v$ and this is called an active transformation.

If you don't change the vector but rotate the axis of the referenc system, than this is called a passive transformation and it is represented by the inverse matrix $R^{-1}$, in the sense that the coordinates of the old vector in the new reference systems are $v''=R^{-1}v$.

edited Jun 01 '16 at 16:14

answered Jun 01 '16 at 16:01

Emilio Novati

62,675

I edited my question. why is that rotation about y axis gives wrong answer and rotation about z axis gives right answer? – user65452 Jun 01 '16 at 16:23
I don't understand your comment. Anyway, the difference between active and passive rotation is the same for any axis of rotation. – Emilio Novati Jun 01 '16 at 16:41
Oh. well, I was using wrong matrix. see my edited question. – user65452 Jun 01 '16 at 16:47

score 3 · Accepted Answer · answered Jun 01 '16 at 16:07

3

@Emilio Novati Explained very well about the rotation. But I spent some time draw this picture, so I'll post it.

You misunderstood the rotation matrix. You should rotate the vector counterclockwisely, instead of rotate the coordinate system.

answered Jun 01 '16 at 16:07

KittyL

16,965

I edited my question. can you explain to me? – user65452 Jun 01 '16 at 16:20
Well, I solved my case. I think your answer gave me a hint. – user65452 Jun 01 '16 at 16:35
@user65452: Notice that your final matrices A.1, A.2 and A.3 are in fact the $R^{-1}$ mentioned in Emilio Novati's answer. So to perform the rotation of vector, you should use the matrix that switches the signs of $\sin\theta$. Anyway your book is definitely incorrect. – KittyL Jun 01 '16 at 16:50

score 1 · Answer 3 · answered Jun 01 '16 at 15:52

1

I believe that you are viewing the problem backwards. The matrix $$ A=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{pmatrix} $$ rotates a vector into a new, rotated frame, according to what you are describing with your images. However, what you are asking is, "What matrix brings me from the rotated frame back to the original frame", which would be the inverse of $A$, i.e. $$ A^{-1} = \begin{pmatrix} 0 & 0 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}. $$

answered Jun 01 '16 at 15:52

ekkilop

2,278

the rotation of a vector along the Y axis by an angle $\theta$ is the same rotation of the landmark OXZ along the Y axis by the angle $-\theta$ . i think, this is where there is confusion with the Schema. – m.idaya Jun 01 '16 at 16:13
sorry, the comment for the autor user65452, thanks – m.idaya Jun 01 '16 at 16:15

Confusion in rotation matrix - rotation about $y$ axis

3 Answers3