Contour integral for finding $\int_0^\infty \frac{\ln x}{(x+a)^2+b^2} \, dx$

Question

I can't prove the following result:

$$\displaystyle\int_0^\infty \frac{\ln x}{(x+a)^2+b^2} \, dx=\frac{\ln \sqrt{a^2+b^2}}{b}\arctan\frac{b}{a} \text{ for all } a,b \in \mathbb{R}.$$

Well, I consider $\displaystyle\int_C \frac{\operatorname{Ln} z}{(z+a)^2+b^2} \, dz$ where $C$ is the usual contour for this kind of integral with logarithm (actually, I don't know if I'm right). So, assuming there is a simple pole inside the interior $C$, I apply the residue theorem as:

$$\begin{align}\int_{C}\frac{\operatorname{Ln} z}{(z+a)^2+b^2} \, dz&= 2\pi i\left(\lim_{z\to-a+ib}\dfrac{(z+a-ib) \operatorname{Ln} z}{(z+a-ib)(z+a+ib)}\right)\\ \\ &=\frac{\pi}{b} \operatorname{Ln} (-a+ib)=\frac{\pi}{b}(\ln (\sqrt{a^2+b^2})+i\arg (-a+ib))\end{align}$$

Now, I must consider estimations of integrals on each semicircle, however I have not idea how I can reach it.

Thanks for any hint.

Answer 1

Note: my solution works only for $a>0,\,b\neq0$. Consider the function $$f\left(z\right)=\frac{\log^{2}\left(z\right)}{\left(z-a\right)^{2}+b^{2}} $$ and the branch of the logarithm corresponding to $-\pi<\arg\left(z\right)\leq\pi.$ Take the keyhole contour and define $\Gamma$ and $\gamma$ respectively the large circumference of radius $R$ and the small circumference of radius $\rho$.

We note that $$\left|\int_{\Gamma}f\left(z\right)dz\right|\leq\frac{\log^{2}\left(R\right)+\pi^{2}}{\left(R-\left|a\right|\right)^{2}-b^{2}}2\pi R\underset{R\rightarrow\infty}{\rightarrow}0 $$ and $$\left|\int_{\gamma}f\left(z\right)dz\right|\leq\frac{\log^{2}\left(\rho\right)+\pi^{2}}{\left|\left(\rho-\left|a\right|\right)^{2}-b^{2}\right| }2\pi\rho\underset{\rho\rightarrow0}{\rightarrow}0. $$ So we have $$2\pi i\left(\textrm{Res}_{z=a+ib}\frac{\log^{2}\left(z\right)}{\left(z-a\right)^{2}+b^{2}}+\textrm{Res}_{z=a-ib}\frac{\log^{2}\left(z\right)}{\left(z-a\right)^{2}+b^{2}}\right) $$ $$=\int_{0}^{\infty}\frac{\log^{2}\left(-x+i\epsilon\right)}{\left(-x+i\epsilon-a\right)^{2}+b^{2}}dx-\int_{0}^{\infty}\frac{\log^{2}\left(-x-i\epsilon\right)}{\left(-x-i\epsilon-a\right)^{2}+b^{2}}dx $$ $$\underset{\epsilon\rightarrow0}{\rightarrow}\int_{0}^{\infty}\frac{\left(\log\left(x\right)+i\pi\right)^{2}-\left(\log\left(x\right)-i\pi\right)^{2}}{\left(x+a\right)^{2}+b^{2}}dx $$ $$=4\pi i\int_{0}^{\infty}\frac{\log\left(x\right)}{\left(x+a\right)^{2}+b^{2}}dx $$ and for the other part we have $$\textrm{Res}_{z=a+ib}\frac{\log^{2}\left(z\right)}{\left(z-a\right)^{2}+b^{2}}+\textrm{Res}_{z=a-ib}\frac{\log^{2}\left(z\right)}{\left(z-a\right)^{2}+b^{2}}=\frac{\log^{2}\left(a+ib\right)-\log^{2}\left(a-ib\right)}{2ib}. $$ Now if we assume that $a>0 $ we have $$\frac{\left(\log\left(\sqrt{a^{2}+b^{2}}\right)+i\arg\left(a+ib\right)\right)^{2}-\left(\log\left(\sqrt{a^{2}+b^{2}}\right)+i\arg\left(a-ib\right)\right)^{2}}{2ib} \tag{1}$$ $$=\frac{2\log\left(\sqrt{a^{2}+b^{2}}\right)\arctan\left(\frac{b}{a}\right)}{b}. $$ Hence

$$\int_{0}^{\infty}\frac{\log\left(x\right)}{\left(x+a\right)^{2}+b^{2}}dx=\frac{\log\left(\sqrt{a^{2}+b^{2}}\right)\arctan\left(\frac{b}{a}\right)}{b}. $$

Addendum: the identity holds only if $a>0 $. If we assume $a<0$ from $(1)$ we have

$$\int_{0}^{\infty}\frac{\log\left(x\right)}{\left(x+a\right)^{2}+b^{2}}dx=\frac{\log\left(\sqrt{a^{2}+b^{2}}\right)\left(\pi-\arctan\left(\frac{b}{a}\right)\right)}{b}. $$

Answer 2

An alternative, real-analytic solution by symmetry only.

$$ \int_{0}^{+\infty}\frac{\log x}{x^2+2ax+(a^2+b^2)}\stackrel{x\mapsto u\sqrt{a^2+b^2}}{=}\frac{1}{\sqrt{a^2+b^2}}\int_{0}^{+\infty}\frac{\log u+\log\sqrt{a^2+b^2}}{u^2+\frac{2a}{\sqrt{a^2+b^2}}u+1}\,du $$ and since the polynomial $p(u)=u^2+\frac{2a}{\sqrt{a^2+b^2}}u+1$ is quadratic and palindromic,
$\int_{0}^{+\infty}\frac{\log u}{p(u)}\,du=0$ by the substitution $u\mapsto \frac{1}{u}$. This leaves us with the elementary integral $$ \int_{0}^{+\infty}\frac{du}{u^2+2Du+1}=\int_{D}^{+\infty}\frac{du}{u^2+(1-D^2)}=\frac{1}{\sqrt{1-D^2}}\,\left(\frac{\pi}{2}-\arctan\frac{D}{\sqrt{1-D^2}}\right) $$ for any $D\in(-1,1)$. By letting $D=\frac{a}{\sqrt{a^2+b^2}}$ we get $$\int_{0}^{+\infty}\frac{\log x}{(x+a)^2+b^2}=\frac{\log\sqrt{a^2+b^2}}{|b|}\left[\frac{\pi}{2}-\arctan\left(\frac{a}{|b|}\right)\right] $$ for any $b\neq 0$. If $b=0$ the LHS is convergent only for $a>0$, and in such a case it equals $\frac{\log a}{a}$.

Answer 3

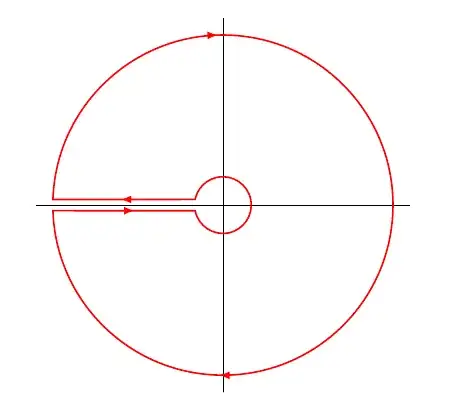
Let's compute the general case:

$$I=\int_0^\infty \frac{a\cdot x^s\ln^n x}{(x+a)^2+b^2}~dx,~~~~~~a\ge0,b\ge0\tag{1}$$

Define

$$F=\int_0^\infty \frac{a\cdot x^s}{(x+a)^2+b^2}~dx,~~~~~-1<s<1$$

hence

$$I=\frac{d^nF}{ds^n}~~~~~\text{and}~~~~~\int_0^\infty \frac{a\ln^n x}{(x+a)^2+b^2}dx=\lim_{s\to0}\frac{d^nF}{ds^n}\tag{2}$$

Next, use the keyhole contour to compute $F$

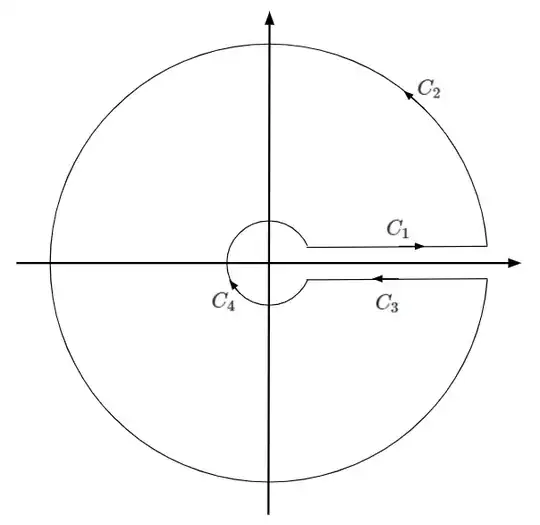
Choose the branch cut along the positive x-axis, where $\arg(z)\in [0,2\pi)$. The integral on $C_2$ vanishes when $s<1$, and the integral on $C_4$ vanishes when $s>-1$. We have two simple poles at $z_1=-a+bi, z_2=-a-bi$

$$\int_{C_1}+\int_{C_2}+\int_{C_3}+\int_{C_4}f(z)dz=2\pi i\sum_{k=1}^2 \text{Res}(z_k)$$

where $\displaystyle f(z)=\frac{a\cdot z^s}{(z+a)^2+b^2}$, we get

$$\left(1-e^{2\pi s i}\right)F=2\pi i\left( \frac{(a^2+b^2)^{s/2}e^{i\theta s}}{2i} +\frac{(a^2+b^2)^{s/2}e^{i(2\pi-\theta) s}}{-2i} \right)$$

where $\displaystyle\theta=\pi-\arctan\left(\frac ba\right)$, simplify and get

$$F=\frac{\pi(a^2+b^2)^{s/2}\sin\left(s\cdot \arctan\left(\frac ba\right) \right)}{\sin(\pi s)}\tag{3}$$

Now, from (2), we get

$$\boxed{\int_0^\infty \frac{a\ln^n x}{(x+a)^2+b^2}~dx=\lim_{\color{red}s\to0}\frac{d^n}{d\color{red}s^n}\left(\frac{\pi(a^2+b^2)^{\color{red}s/2}\cdot\sin\left(\color{red}s\cdot \arctan\left(\frac ba\right) \right)}{\sin(\pi \color{red}s)}\right)}\tag{4}$$

Here are some results generated by (4)

$$\begin{align} n&=0,~~ \int_0^\infty \frac{a}{(x+a)^2+b^2}~dx=\arctan\left(\frac ba\right)\\ \\ n&=1,~~ \int_0^\infty \frac{a \ln x}{(x+a)^2+b^2}~dx=\frac12\arctan\left(\frac ba\right)\ln(a^2+b^2)\\ \\ n&=2,~~ \int_0^\infty \frac{a \ln^2x}{(x+a)^2+b^2}~dx=\frac1{12}\arctan\left(\frac ba\right)\left(4\pi^2-4\arctan^2\left(\frac ba\right)+3\ln^2(a^2+b^2)\right)\\ \\ n&=3,\\ \\ &\int_0^\infty \frac{a \ln^3x}{(x+a)^2+b^2}dx=\frac1{8}\arctan\left(\frac ba\right)\ln(a^2+b^2)\left(4\pi^2-4\arctan^2\left(\frac ba\right)+\ln^2(a^2+b^2)\right)\\ \end{align}$$