2

I was working through Can the composition of two non-invertible functions be invertible? For the image below is $f \circ g$ invertible?

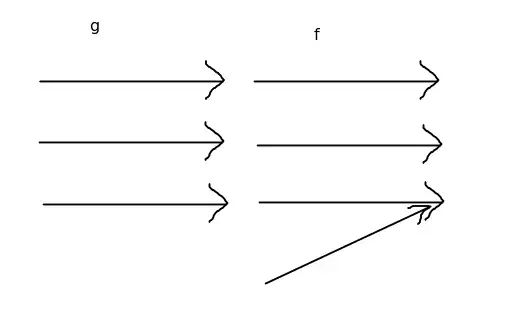
The arrows signify mapping. I have not drawn the nodes but assume they are present.

Thanks!

Tarun Kumar
  • 25
  • if (f o g) is invertible then so is g, thus, strictly speaking, your example is not the composition of "two non-invertible" functions but rather of "an invertible and a nob-invertible function". – D.F.F Jun 14 '16 at 07:55
  • @D.F.F The original question in the text ask for a counter example for Suppose that f and g are functions and f ◦ g is invertible. Then f and g are invertible. I don't think both can be non invertible or can they be? – Tarun Kumar Jun 14 '16 at 08:10
  • They can't as the injectivity of f o g implies that g is injective as well. – D.F.F Jun 14 '16 at 08:46
  • @D.F.F Actually, since invertible means bijective, yes, they can both be non invertible. And the example shows this. $g$ is not invertible. – 5xum Jun 14 '16 at 15:21
  • @ 5xum I assumed invertible means injective (which makes sense if a function is understood as a set of ordered pairs). – D.F.F Jun 14 '16 at 16:39

2 Answers2

1

Yes, good job! You've correctly constructed a counterexample that demonstrates how $f \circ g$ can be invertible even though $f$ is not invertible (since $f$ only needs to be invertible when its domain is restricted to the range of $g$).

Adriano
  • 41,576
0

Your counterexample is good.

You can see in your example the two properties in action:

  • If $f\circ g$ is surjective, then $f$ must be surjective (and yours is), but $g$ doesn't need to be surjective (and yours is not)
  • If $f\circ g$ is injective, then $g$ must be injective (yours is), but $f$ does not need to be injective (yours is not)
5xum
  • 123,496
  • 6
  • 128
  • 204