9

This should be really straightforward from the formula, but somehow I'm having trouble understanding the density of a Dirichlet distribution with $\alpha = [1, 1, ... 1] \in R^k$, which is a uniform distribution over the $k-1$ dimensional simplex. For example, $Dir(x;[1,1,1])$ is the same as a uniform distribution over the triangle with vertices $[0,0,1], [0,1,0]$, and $[0,0,1]$ (see pic below).

Uniform distribution over equilateral triangle

Since there's 1 unit of probability mass uniformly spread over the triangle, I thought the density should simply be $1/Area(triangle)=2/\sqrt(3)$; but the formula is giving me $Dir(x;[1,1,1])=2$. How come?

Yibo Yang
  • 1,556
  • Also see this answer to basically the same question: https://math.stackexchange.com/a/3781574/257082 The key thing to realize is that the density is actually a function defined over $\mathbb{R}^{k-1}$, rather than $\mathbb{R}^{k}$ as Wikipedia would suggest. – Yibo Yang Feb 03 '21 at 07:32

1 Answers1

9

I'm assuming the definitions written here.

The density function of the variable $X$ associated to $\mathrm{Dir}(\alpha)$ (where $\alpha = [\alpha_1,\cdots,\alpha_k]^{\top} \overset{def}= [1,\cdots,1]^{\top} \in \mathbb R^k$) is given by $$ f(x_1,\cdots,x_k,1,\cdots,1) = \frac 1{B(\alpha)} \prod_{i=1}^k x_i^{\alpha_i - 1} = \frac 1{B(\alpha)} = \frac{\Gamma(k)}{\Gamma(1)^k} = (k-1)! $$ So your computation $\mathrm{Dir}(x, [1,1,1]) = 2$ is correct.

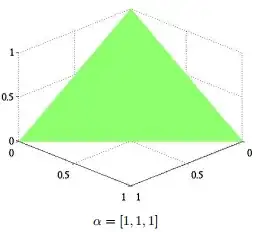
For obvious symmetry reasons, the triangle will be equilateral. The length of one of its sides is $\|[1,0,0] - [0,1,0]\| = \sqrt 2$, hence its area is equal to $6/(4 \sqrt 3) = \sqrt 3/2$.

Both formulas are correct. The issue is that you are computing the area of the triangle using the "area" measure of the triangle, not the Lebesgue measure of the space used to compute the density, namely $[0,1]^{k-1}$. The factor $(\sqrt 3/2)/2 = \sqrt 3/4$) is the Jacobian involved in the change of variables to integrate a function defined on your green triangle with respect to the coordinates $x_1,\cdots,x_{k-1}$. The reason for this is that in the multiple integral $$ B(\alpha_1,\cdots,\alpha_k) = \int_{x_1 = 0}^1 \cdots \int_{x_{k-1}=0}^1 x_1^{\alpha_1-1} \cdots x_{k-1}^{\alpha_{k-1}-1} (1-x_1 - \cdots - x_{k-1})^{\alpha_k-1} dx_1 \cdots dx_{k-1}, $$ we are integrating with respect to arguments which are not variables living on the surface of the triangle where the random variable lives, but rather its projection on the hyperplane $x_k = 0$, which has area $2$ (in the case $k=2$).

Hope that helps,

Patrick Da Silva
  • 41,413
  • 1
    I think there's a slight issue with the limits of integration in the integral (need to restrict to the simplex). And in the case $k=2$, $B(\alpha_1=1, \alpha_2=1) = \int_{x_1=0}^1 \int_{x_2=0}^{1-x_1} x_1^0 x_2^0 (1-x_1-x_2)^0 d x_2 d x_1 = \frac{1}{2}$. – Yibo Yang Feb 03 '21 at 07:41