As drhab noted, given the value of $X_1$, the remaining numbers are a uniformly random sample of size $5$ without replacement from the numbers above $X_1$.
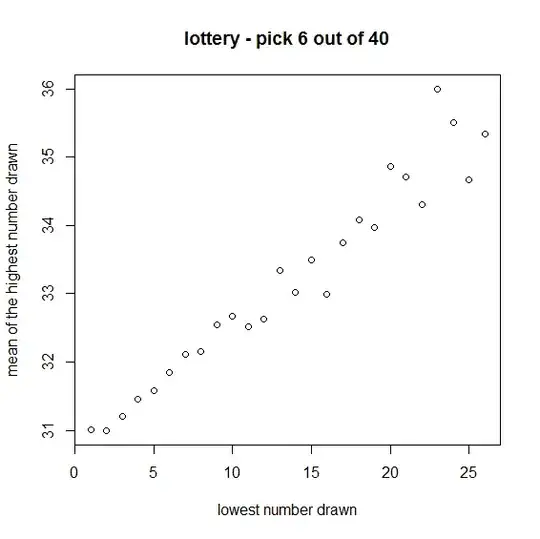
To find the mean of the maximum of $k$ distinct numbers drawn from $1$ to $n$, take $n-k$ white balls, $k$ red balls and $1$ yellow ball, arrange them in a uniformly random permutation in a circle, and remove the yellow ball to obtain a linear arrangement, with the positions of the $k$ red balls corresponding to the $k$ numbers drawn. By symmetry, all $k+1$ segments between the $k+1$ coloured balls have the same expected length, so the expected value of the highest number drawn is $n-\frac{n-k}{k+1}$.
To find the variance, consider the sum $X=\sum_iX_i$ of $n-k$ indicator variables, where each variable is $1$ if the corresponding white ball is to the right of the last red ball and $0$ if it's to the left. Then the highest number drawn is $n-X$, and $E[X]=\frac{n-k}{k+1}$ as derived above. Now calculate
\begin{align}
\mathbb E[X^2]
&=
\mathbb E\left[\left(\sum_iX_i\right)^2\right]
\\
&=
\mathbb E\left[\sum_iX_i\right]+\mathbb E\left[\sum_{i\ne j}X_iX_j\right]
\\
&=
\frac{n-k}{k+1}+(n-k)(n-k-1)\mathbb E[X_1X_2]
\\
&=
\frac{n-k}{k+1}+(n-k)(n-k-1)\frac1{\binom{k+2}2}
\\
&=
\frac{n-k}{k+1}\left(1+2\cdot\frac{n-k-1}{k+2}\right)\;.
\end{align}
Then
\begin{align}
\operatorname{Var}[X]
&=\mathbb E[X^2]-E[X]^2
\\
&=
\frac{n-k}{k+1}\left(1+2\cdot\frac{n-k-1}{k+2}-\frac{n-k}{k+1}\right)
\\
&=
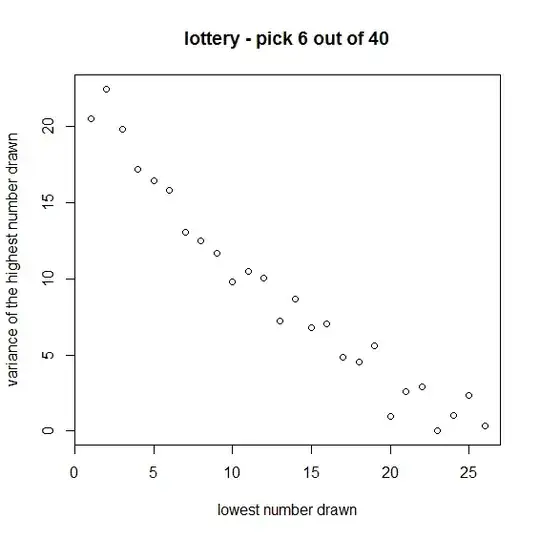
\frac{k(n-k)(n+1)}{(k+1)^2(k+2)}\;,
\end{align}
which is also the variance of $n-X$, that is, of the highest number drawn.
Note that no sums over the distribution had to be computed in the process, only one probability, the probability $\frac1{\binom{k+2}2}$ for two white balls to be to the right of all $k$ red balls.