Geometric proof re: parabola focus and potential calculus connection

Question

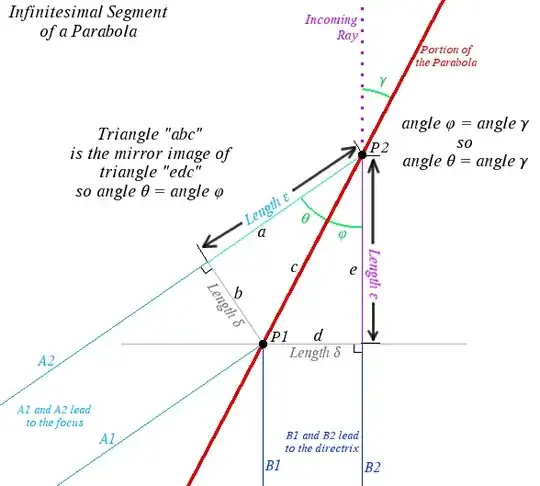
The image above is a proof that light traveling with an orientation perpendicular to the directrix into a parabola will be reflected to the focus of the parabola. (In the diagram, the purple dotted line labeled "Incoming Ray" bounces off the solid red line and travels along the segment P2 to A2.)

The proof relies upon basic geometry (eg, Pythagorean Theorem) and one critical assumption: that the segments extending to the focus from points P1 and P2 (both on the parabola) are "essentially" parallel given the choice of P1 and P2. From this assumption, it follows that segment a is equal to segment e, and therefore b is equal to d. (Hopefully the rest of the proof is clear enough from there.)

But here's the rub: to use the Pythagorean Theorem, we need to have the segment c be straight. If it curves at all, we cannot conclude that b = d and we thus can't say anything about the relevant angles being congruent. The segment connecting any two points lying on a parabola will be curved, albeit perhaps by a very small amount. I don't see how we can "zoom in" so that we're looking at an "infinitesimal" segment of a parabola and have a straight segment connecting the two points in question; there will always and everywhere be curvature.

It seems correct to say that, passing to the limit, c approaches "straightness" as P1 approaches P2. Can we construct a more rigorous argument, along the lines used in this diagram, with the tools of limits/calculus?

Source of diagram: http://www.physicsinsights.org/parabola_focus.html

Answer 1

If you use calculus then the problem is very easy. You don't need those geometric argument but instead you require some algebraic manipulations.

---

Consider the parabola $y^{2} = 4ax$ with focus at $(a, 0)$ and directrix $x = -a$. A line perpendicular to the directrix is of the form $y = k$ which meets the parabola in point $P = (k^{2}/4a, k)$. The slope of the tangent at this point is given by $y' = \sqrt{a/x} = 2a/k$ and hence the slope of normal at this point is $-k/2a$.

Consider the line joining focus $F = (a, 0)$ and the point $P = (k^{2}/4a, k)$. Its slope is given by $$\frac{4ak}{k^{2} - 4a^{2}}$$ Thus angle $\theta$ between the line PF and normal is given by $$\tan \theta = \left|\dfrac{\dfrac{4ak}{k^{2} - 4a^{2}} + \dfrac{k}{2a}}{1 - \dfrac{4ak}{k^{2} - 4a^{2}} \cdot \dfrac{k}{2a}}\right| = \frac{4a^{2}k + k^{3}}{2ak^{2} + 8a^{3}} = \frac{k}{2a}$$ And clearly the angle $\alpha$ between line $PF$ and line $y = k$ is also given by $\tan \alpha = k/2a$ so it follows that the line $y = k$ is reflected as line $PF$ by the parabola when it hits points $P$.

The above proof can be simplified if we combine calculus and geometry. See this paper.