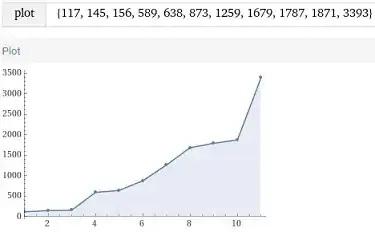
Here is the list of 27 known solutions found before 2010 and below a bound. (Update: As of 2023, there are 27+4 = 31 known solutions below $10^{28}$, the 4 found in 2015 by Bremner and all higher than #20 in this list.)
The list was brute-forced only up to $2\times10^9$ . Other cases were discovered using elliptic curves, which doesn't guarantee completeness of the list above 2 billion. We can notice that the pattern is less regular than that of PPT. It is neither linear not exponential. Conclusions derived from 30 examples may not be accurate. Table below is of the form $(d;c,b,a)$ for $d^4=c^4+b^4+a^4$.
1] 422481; 414560, 217519, 95800 (Roger Frye, 1988)
2] 2813001; 2767624, 1390400, 673865 (Allan MacLeod 1997)
3] 8707481; 8332208, 5507880, 1705575 (D.J. Bernstein, 2001)
4] 12197457; 11289040, 8282543, 5870000 (D.J. Bernstein, 2001)
5] 16003017; 14173720, 12552200, 4479031 (D.J. Bernstein, 2001)
6] 16430513; 16281009, 7028600, 3642840 (D.J. Bernstein, 2001)
7] 20615673; 18796760, 15365639, 2682440 (Noam Elkies, 1986)
8] 44310257; 41084175, 31669120, 2164632 (Robert Gerbicz, 11/08/2006)
9] 68711097; 65932985, 42878560, 10409096 (Robert Gerbicz, 11/08/2006)
10] 117112081; 106161120, 87865617, 34918520 (Robert Gerbicz, 11/02/2006)
11] 145087793; 122055375, 121952168, 1841160 (Juergen Rathmann, 5/31/2007)
12] 156646737; 146627384, 108644015, 27450160 (Juergen Rathmann, 6/1/2007)
13] 589845921; 582665296, 260052385, 186668000 (Seiji Tomita, 03/13/2006)
14] 638523249; 630662624, 275156240, 219076465 (Allan MacLeod,1998)
15] 873822121; 769321280, 606710871, 558424440 (Robert Gerbicz, Leonid Durman, Yuri Radaev, Alexey Zubkov 11/2/2007)
16] 1259768473; 1166705840, 859396455, 588903336 (Robert Gerbicz, Leonid Durman, Yuri Radaev, Alexey Zubkov 01/25/2008)
17] 1679142729; 1670617271, 632671960, 50237800 (Seiji Tomita, 03/13/2006)
18] 1787882337; 1662997663, 1237796960, 686398000 (Robert Gerbicz, Leonid Durman, Yuri Radaev, Alexey Zubkov 11/2/2007)
19] 1871713857; 1593513080, 1553556440, 92622401 (Robert Gerbicz, Leonid Durman, Yuri Radaev, Alexey Zubkov 10/31/2007)
20] 3393603777; 3134081336, 2448718655, 664793200 (Seiji Tomita, 01/28/2007)
21] 12558554489; 11988496761, 7813353720, 4707813440 (Andrew Bremner, 2015)
22] 15434547801; 15355831360, 5821981400, 140976551 (Seiji Tomita, 10/24/2007)
23] 1367141947873; 1226022682752, 1047978087905, 408600530760 (Andrew Bremner, 2015)
24] 5062297699257; 4987588419655, 2480452675600, 502038853976 (Seiji Tomita, 05/15/2008)
25] 29999857938609; 27239791692640, 22495595284040, 7592431981391 (Seiji Tomita, 03/13/2006)
26] 573646321871961; 514818101299289, 440804942580160, 130064300991400 (Seiji Tomita, 09/15/2008)
27] 20249506709579721; 18565945114216720, 14890026433468471, 3579087147375440 (Seiji Tomita, 08/13/2008)
28] 62940516903410601; 56827813308111785, 47886740272114976, 8813425670440240 (Seiji Tomita, 08/13/2008)
29] 2778996090487120353; 2556827383749699103, 2024155336530384440, 585715960903147640 (Andrew Bremner, 2015)
30] 31293260543726494476580617; 27386104940472276169105720, 25024939958628554701755145, 8089277164034877786318544 (Andrew Bremner, 2015)
31] 1677479490238223823661446513; 1507524066882038472584786800, 1288056982586427591062203384, 169218021322170204480680305 (Seiji Tomita, 03/13/2006)