1

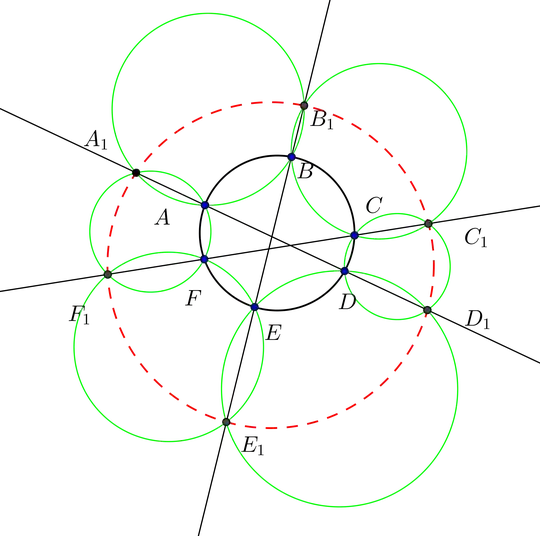
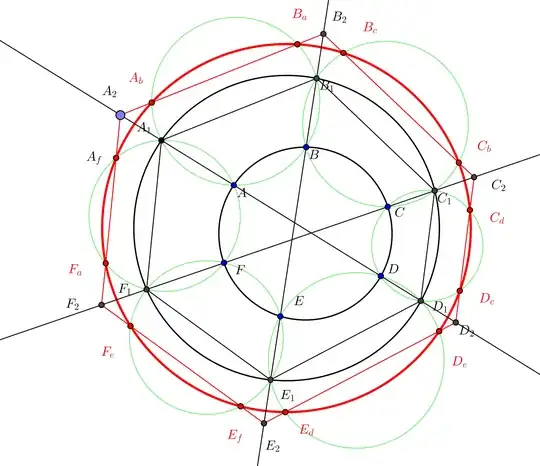
When I research this problem A chain of six circles associated with a cyclic hexagon. I found the followings result.

Let $ABCDEF$ be a cyclic hexagon. Let $A_1$ be any point on $AD$, the circle $(A_1AB)$ meets $BE$ again at $B_1$. The circle $(B_1BC)$ meets $CF$ again at $C_1$. The circle $(C_1CD)$ meets $AD$ again at $D_1$. The circle $(D_1DE)$ meets $BE$ again at $E_1$. The circle $(E_1EF)$ meets $CF$ again at $F_1$. Then show that $F_1, F, A, A_1$ lie on a circle and six points $A_1, B_1, C_1, D_1, E_1, F_1$ lie on a circle.

enter image description here

My question: Let $A_2, D_2 \in AD; B_2, E_2 \in BE, C_2, F_2 \in CF$ such that such that the sidelines of the hexagon $A_2B_2C_2D_2E_2F_2$ parallel to the sidelines of $A_1B_1C_1D_1E_1F_1$ respectively. Let line $A_2B_2$ meets the circle $(ABB_1A_1)$ at two points $A_b, B_a$. Define $B_c$, $C_b$, $C_d, D_c$, $D_e, E_d$, $E_f, F_e$, $F_a, A_f$ cyclically (cyclically meen: define the same, define similarly). Then show that twelve points: $A_b, B_a$, $B_c$, $C_b$, $C_d, D_c$, $D_e, E_d$, $E_f, F_e$, $F_a, A_f$ lie on a circle.

enter image description here

Community
  • 1
Oai Thanh Đào
  • 1,326

1 Answers1

0

From radical center theorem we get that $A_bB_aB_cC_b$ is cyclic and from other arguments that it's center coincides with the center of $(A_1B_1C_1)$. Same for other quadrangles. $\Box$

solver6
  • 141