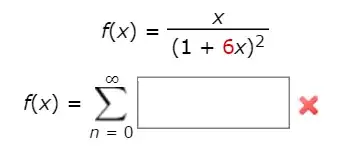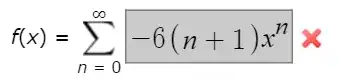I'm not sure how to handle this problem. I got that the radius of convergence was 1/6, but I don't know how to represent the function as a power series.
I can modify it to look like the following:
x * 1/(1-(-6x))^2
I thought this would be the power series but apparently not.
OK, let us start from the well-known formula
$$\frac{1}{1+x}=\sum_{n=0}^{\infty}(-1)^nx^n, \quad |x|<1 \tag{1}$$
Next we obtain the series expansion
$$\begin{align} \frac{1}{(1+x)^2} &= -\frac{d}{dx}\frac{1}{1+x} = - \frac{d}{dx} \sum_{n=0}^{\infty}(-1)^nx^n \\ &= -\sum_{n=0}^{\infty}n(-1)^n x^{n-1} = \sum_{n=0}^{\infty}n(-1)^{n+1}x^{n-1} \\ &= \sum_{n=1}^{\infty}n(-1)^{n+1}x^{n-1}, \quad |x|<1 \end{align} \tag{2}$$
Multiply $(2)$ by $x$ to get
$$\begin{align} \frac{x}{(1+x)^2} &= \sum_{n=1}^{\infty}n (-1)^{n-1} x^n, \quad |x|<1 \end{align} \tag{3}$$
Replacing $x$ with $6x$ in $(3)$ and multiplying by $\dfrac{1}{6}$ gives the final result
$$\frac{x}{(1+6x)^2}=\sum_{n=1}^{\infty}n (-1)^{n-1} x^n, \quad |x|<\frac 16 \tag{4}$$
Applying the formula for the binomial series representation we obtain \begin{align*} \frac{x}{(1+6x)^2}&=x\sum_{n=0}^\infty\binom{-2}{n}(6x)^n\tag{1}\\ &=x\sum_{n=0}^\infty\binom{n+1}{1}(-6x)^n\tag{2}\\ &=\sum_{n=0}^\infty(n+1)(-6)^nx^{n+1}\\ &=\sum_{n=1}^\infty(-6)^{n-1}nx^n\qquad\qquad\qquad |x|<\frac{1}{6}\tag{3} \end{align*}
Comment:
In (1) we apply the binomial series representation with $\alpha=-2$ \begin{align*} (1+x)^\alpha=\sum_{n=0}^\infty\binom{\alpha}{n}x^n\qquad\qquad |x|<1 \end{align*}
In (2) we use the binomial identity \begin{align*} \binom{-n}{k}=\binom{n+k-1}{n-1}(-1)^k \end{align*}
In (3) we shift the index by one to obtain powers $x^n$ again
Observe that : $\dfrac{x}{(1+6x)^2}= x\dfrac{d}{dx}\left(-\dfrac{1}{6(1+6x)}\right)$,and you have $\dfrac{1}{1+6x} = 1+(-6x) + (-6x)^2 +\cdots , |x| < \frac{1}{6}$
