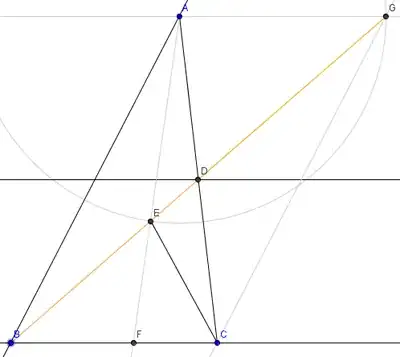
This question seems tricky and I frankly don't know how to start. I will be grateful if someone can provide a solution.
We have a triangle $ABC$ and there is a point $F$ on $BC$ such that $AF$ intersects the median $BD$ at $E$. If $AE=BC$ how do we prove that triangle $BEF$ is isosceles?
I think this has to do with ratios of sides, but I'm not getting any where. I drew a graph as accurately as I could and I am pretty confident that the objective of the problem is to somehow show that $EF$ equals $BF$, but I have no clue. Thanks!