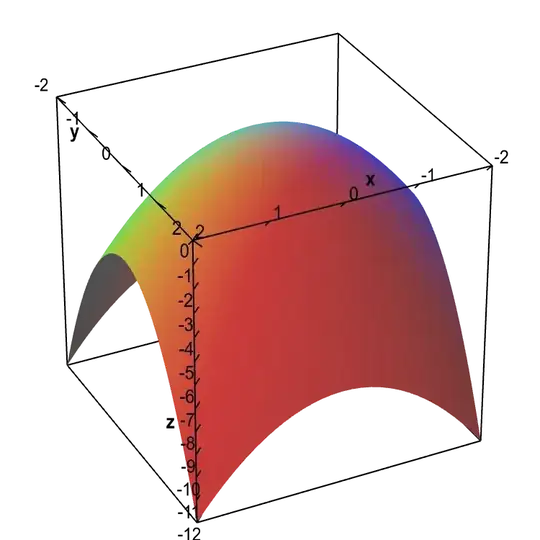1

Let $C \subset \mathbb{R}^{n}$ denote a non-compact convex subset of the Euclidean space $\mathbb{R}^n$ and $f : C \to \mathbb{R}^n$ a continuous function. What are the conditions to ensure that $f$ has a minimum on $C$ ?

If $C$ was compact, it would be OK.

If $f$ is convex, I guess something could be said.

Consider $C = ]0,+\infty[$ and $f(x) = x - \ln(x)$ for all $x \in C$. Then $f$ satisfies : $$ \lim \limits_{\substack{x \to 0 \\ x > 0}} f(x) = \lim \limits_{x \to +\infty} f(x) = +\infty \tag{$\star$} $$ $f$ is continuous (and convex) on $C$. The conditions $(\star)$ are enough to ensure that $f$ has a minimum on $C$. Indeed, by ($\star$), one can find $m,M \in C$ such that $f$ is arbitrarily large on $C \smallsetminus [m,M]$. By continuity, since $[m,M]$ is compact, $f$ has a minimum on $[m,M]$ and therefore on $C$.

Does that follow from a theorem I don't know ? How would $(\star$) generalize in higher dimension (say, for $C = ]0,+\infty[^n \times \mathbb{R}^p$) ?

Odile
  • 1,171
  • 8
  • 10
  • 1
    If the domain is $\mathbb{R}^n$ then it is enough that $f$ is strongly convex: http://math.stackexchange.com/questions/1035110/does-every-strongly-convex-function-has-a-stationary-point – smcc Aug 09 '16 at 14:24

2 Answers2

2

Consider the convex subset of $\mathbb{R}^{n+1}$ $C$ defined by $$C := \{ x \in \mathbb{R}^{n+1}: x_{n+1} \le -x_1^2 - \dots -x_n^2\} $$ (for $n=2$ this is the region under a negative paraboloid).

Then this is a non-compact, convex subset of $\mathbb{R}^{n+1}$, but in general it will not be possible to find a minimum on it, even for continuous functions. For example, the function $f(x_1, \dots, x_{n+1})= -x_1^2-\dots-x_n^2+0\cdot x_{n+1}$ has no minimum on $C$.

Obviously there exists a maximum, and (for smooth functions) using gradient descent we will be guaranteed to find local extrema.

If we had a function which was strictly positive then we could find a maximum, but then for $C'$ which is a suitable reflection of $C$ (namely $\{ x \in \mathbb{R}^{n+1}: x_{n+1} \ge x_1^2 + \dots x_n^2\}$) we would be guaranteed a minimum but no maxima for such functions. So I don't think that in general it will be possible to find a condition without tailoring it specifically for the given non-compact convex subset which you are interested in.

EDIT: (1) Looking at smcc's comment above, my example seems to just be a special case of the result he mentions: Does every strongly convex function has a stationary point?. Quadratic functions are strongly convex since $f_{x_ix_i}(x) = 2 >0$ for any $x \in \mathbb{R}^n$, so it follows immediately that the above example is a special case of the general result shown in the linked to post.

(2) This condition isn't related to the convexity of the set, but if your subset is a topological manifold, then there always exists an exhaustion by compact sets. See, for example here Existence of exhaustion by compact sets or Lee's book Introduction to Topological Manifolds.

So if you take a compact subset $K_1$ of your set $C$, and find an extremum $x \in K_1$, and then create an exhaustion by compacts sets $(K_n)$ of $C$ (with $K_1=K_1$ of course) such that $x$ is an extremum for each $K_n$, then $x$ will be an extremum for $C$.

Obviously good points to check for extrema satisfying such an exhaustion property are extreme points of your convex subset. This works at least for the very naive example given above, and perhaps may be a way to prove the result regarding strongly convex functions having a single stationary point.

(3) This paper might be of interest to you.

enter image description here

Community
  • 1
Chill2Macht
  • 20,920
  • Thank you for the example ! If we add the condition that $\Vert f(x) \Vert$ must "explode" on $C$, in some sense, then your function $f$ shall have a minimum on a reflection of $C$ ($\lbrace x_{n+1} > x_{1}^{2} + \ldots + x_{n}^{2} \rbrace$). Does that follow from some theorem ? – Odile Aug 09 '16 at 14:25
  • I think one way you could show is that you can use exhaustion by compact sets (https://en.wikipedia.org/wiki/Exhaustion_by_compact_sets), so if you have that there is a minimum at the origin for all compact subsets of the reflection containing the origin, then it will be the minimum for the entire set. An exhaustion by compact sets exists because the set is a topological manifold, see this question: http://math.stackexchange.com/questions/1360900/existence-of-exhaustion-by-compact-sets – Chill2Macht Aug 09 '16 at 15:36
  • Actually I guess this gives you a criterion, although it isn't necessarily related to the convexity of the set; I will edit my post to reflect this fact. Also another reference showing that topological manifolds have exhaustions by compact sets is Lee's Introduction to Topological Manifolds. – Chill2Macht Aug 09 '16 at 15:38
1

You need better control of the domain/function to say something. On $I=(0,+\infty)$ then function $x\mapsto 1/x-x$ is convex but has no lower bound. On a bounded domain a convex function will have a finite infimum but need not attain that inf in the interior (easy counter examples).

Concerning condition (*): If you happen to know that there is a compact subset $K\subset C$ so that $\inf_{C\setminus K} f > f(a)$ for some $a\in K$ then you are back in business (like in your example). $f$ need not be convex, nor does the domain.

H. H. Rugh
  • 35,236
  • But the function $x\mapsto 1/x-x$ does not satisfy $(\star)$ because $\lim_{x\to\infty} 1/x-x=-\infty$. – smcc Aug 09 '16 at 15:00
  • Correct, but with condition (*) convexity is not necessary. Just saying that convexity as such does not seem related to the problem here. – H. H. Rugh Aug 09 '16 at 16:49