1

I am studying Peterson's book of riemannian geometry and he gives me a metric:

$$g = dt^2 + a^2t^2d\theta^2$$

and asks me to identify which are the spaces when I change $a$.

I never expected anything like this before, how can I think about this problem?

L.F. Cavenaghi
  • 4,651
  • 1
    Is the second term $a^{2} t^{2}, d\theta^{2}$, by chance? :) – Andrew D. Hwang Aug 15 '16 at 22:57
  • 1
    yes! Thank you @AndrewD.Hwang – L.F. Cavenaghi Aug 15 '16 at 23:11
  • 1
    Here are a couple of hints (in addition to the hint implicit in the title): $dt^{2} + t^{2}, d\theta^{2}$ is the flat (Euclidean) metric in polar coordinates. The multiplicative factor $a^{2}$ scales the length of each circle $t = \text{constant}$ without changing its "radius" (distance to the origin), and without changing the local isometry class of the metric (away from the origin). – Andrew D. Hwang Aug 15 '16 at 23:43
  • @Andrew, I will think about it! Thanks – L.F. Cavenaghi Aug 16 '16 at 00:06
  • @AndrewD.Hwang, what does the book mean by cone? It says that for $a>1$ it is a cone. What does it mean? – L.F. Cavenaghi Aug 20 '16 at 23:27
  • 1
    Probably the book meant "for $0 < a < 1$...." (The length of the curve $t = t_{0}$ is $2\pi a^{2} t_{0}$, which must be smaller than $2\pi$ for a circular cone of rotation.) That said, you can make a paper model for the case $1 < a$ by cutting out two paper disks, slitting each along a ray from the center, and attaching one edge of one slit to the "opposing" edge of the other slit, keeping the other two edges free. Now manipulate the model by "opening" the central angle, so that more than $2\pi$ worth of angle comes to the vertex at the center. – Andrew D. Hwang Aug 21 '16 at 00:06

1 Answers1

2

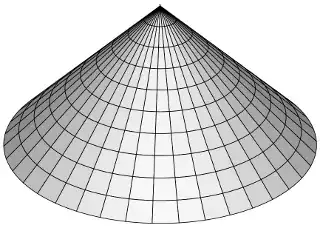
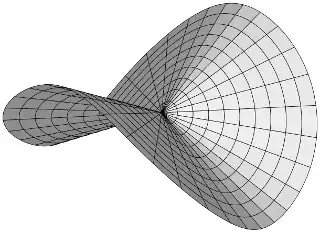
If $0 < a$, the metric $$ g = dt^{2} + a^{2} t^{2}\, d\theta^{2},\qquad 0 < t,\quad 0 \leq \theta \leq 2\pi, $$ is flat, and represents a cone if $0 < a < 1$, a flat plane if $a = 1$, or a "saddle cone" (non-standard term?) if $1 < a$. A cone A saddle cone

Each such metric embeds isometrically in Euclidean $3$-space, and the space of isometric embeddings is infinite-dimensional: Pick a smooth, embedded, constant-speed curve $\gamma$ of length $2\pi a$ on the unit sphere, and define $$ \phi(t, \theta) = t\gamma(\theta). $$ Since $\phi_{t} = \gamma$ lies on the unit sphere and $\phi_{\theta} = t\gamma'$ is tangent to the sphere and has constant speed $a$, the components of the induced metric are $$ E = 1,\qquad F = 0,\qquad G = t^{2} \|\gamma'\|^{2} = a^{2} t^{2}. $$

Andrew D. Hwang
  • 78,195