Evaluate the integral $\int_0^\infty \frac{dx}{\sqrt{(x^3+a^3)(x^3+b^3)}}$

Question

This integral looks a lot like an elliptic integral, but with cubes instead of squares:

$$I(a,b)=\int_0^\infty \frac{dx}{\sqrt{(x^3+a^3)(x^3+b^3)}}$$

Let's consider $a,b>0$ for now.

$$I(a,a)=\int_0^\infty \frac{dx}{x^3+a^3}=\frac{2 \pi}{3 \sqrt{3} a^2}$$

I obtained the general series solution the following way. Choose $a,b$ such that $a \geq b$, then:

$$I(a,b)=\frac{1}{a^2} \int_0^\infty \frac{dt}{\sqrt{(t^3+1)(t^3+b^3/a^3)}}=\frac{1}{a^2} I \left(1, \frac{b}{a} \right)$$

$$\frac{b^3}{a^3}=p, \qquad I \left(1, \frac{b}{a} \right)=I_1(p)$$

$$I_1(p)=\int_0^\infty\frac{dt}{\sqrt{(t^3+1)(t^3+p)}}=2 \frac{d}{dp} J(p)$$

$$J(p)=\int_0^\infty\sqrt{\frac{t^3+p}{t^3+1}}dt=\int_0^\infty\sqrt{1+\frac{p-1}{t^3+1}}dt=$$

$$|p-1| \leq 1$$

$$=\sum_{k=0}^\infty \left( \begin{array}( 1/2 \\ ~k \end{array} \right) (p-1)^k \int_0^\infty \frac{dt}{(t^3+1)^k}$$

Now this is the most problematic part. The first integral of this series diverges. However, it's a constant in $p$, so if we differentiate, it formally disappears:

$$I_1(p)=2 \sum_{k=1}^\infty \left( \begin{array}( 1/2 \\ ~k \end{array} \right) k (p-1)^{k-1} \int_0^\infty \frac{dt}{(t^3+1)^k}$$

Now, every integral in this series converges. The integtals can be computed using the Beta function, if we substitute: $$t^3=\frac{1}{u}-1$$

Finally, we rewrite:

$$I_1(p)=\frac{\Gamma (1/3)}{3 \sqrt{\pi}} \sum_{k=1}^\infty \frac{k^2}{k!^2} \Gamma \left(k- \frac{1}{2}\right) \Gamma \left(k- \frac{1}{3}\right) (1-p)^{k-1}$$

Or, using the Pochhammer symbol:

$$I_1(p)=\frac{2 \pi}{3 \sqrt{3}} \sum_{k=0}^\infty \frac{(k+1)^2}{(k+1)!^2} \left(\frac{1}{2}\right)_k \left(\frac{2}{3}\right)_k (1-p)^k$$

My questions are:

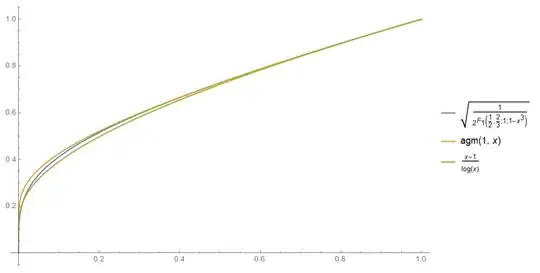
Is the method I used valid (see the 'problematic part')? How to get this series into a Hypergeometric function form?

Is there any 'arithmetic-geometric mean'-like transformation (Landen's transformation) for this integral? How to go about finding it?

If the method I used is correct, it can be used for any integral of the form ($m \geq 2$):

$$I_m(a,b)=\int_0^\infty \frac{dx}{\sqrt{(x^m+a^m)(x^m+b^m)}}$$

Answer 1

It was already shown that $$ I_1(p)=\int_0^\infty \frac{dx}{\sqrt{(x^3+1)(x^3+p)}}=\frac{2 \pi}{3 \sqrt{3}} {_2F_1} \left(\frac{1}{2},\frac{2}{3};1;1-p \right). $$ By transformation 2.11(5) from Erdelyi, Higher transcendental functions (put $z=\frac{1-\sqrt{p}}{1+\sqrt{p}}$) $$ {_2F_1} \left(\frac{1}{2},\frac{2}{3};1;1-p \right)=\left(\frac{2}{1+\sqrt{p}}\right)^{4/3}{_2F_1} \left(\frac{2}{3},\frac{2}{3};1;\left(\frac{1-\sqrt{p}}{1+\sqrt{p}}\right)^{2} \right). $$ By Pfaff's transformation $$ {_2F_1} \left(\frac{2}{3},\frac{2}{3};1;\left(\frac{1-\sqrt{p}}{1+\sqrt{p}}\right)^{2} \right)=\left(\frac{(1+\sqrt{p})^2}{4\sqrt{p}}\right)^{2/3}{_2F_1} \left(\frac{1}{3},\frac{2}{3};1;\frac{(1-\sqrt{p})^2}{-4\sqrt{p}} \right). $$ As a result $$ I_1(p)=\frac{2 \pi}{3 \sqrt{3}p^{1/3}}{_2F_1} \left(\frac{1}{3},\frac{2}{3};1;\frac{(1-\sqrt{p})^2}{-4\sqrt{p}} \right). $$ Now we will use a generalization of AGM found by Borwein and Borwein, A Cubic Counterpart of Jacobi's Identity and the AGM, Transactions of the American Mathematical Society, Vol. 323, No. 2, (1991), pp.691-701 (after correcting for some typos): $$ a_{n+1}=\frac{a_n+2b_n}{3} ,\quad b_{n+1}=\sqrt[3]{b_n\frac{a_n^2+a_nb_n+b_n^2}{3}},\quad a_0=1,\quad b_0=s, $$ $$ \quad AG_3(1,s)=\lim_{n\to\infty} a_n=\frac{1}{{_2F_1} \left(\frac{1}{3},\frac{2}{3};1;1-s^3 \right)}. $$ Using this we get

\begin{align} I_1(p)=\frac{2 \pi}{3 \sqrt{3}~p^{1/3}\cdot AG_3\left(1,\left(\frac{1+\sqrt{p}}{2~\sqrt[4]{p}}\right)^{2/3}\right)}. \end{align}

Answer 2

More generally, with $|p-1|<1$, some experimentation shows that, $$\int_0^\infty \frac{dt}{\sqrt{(t^m+1)(t^m+p)}} = \pi\,\frac{\,_2F_1\big(\tfrac12,\tfrac{m-1}{m};1;1-p\big)}{m\sin\big(\tfrac{\pi}{m}\big)}$$ where the question was just the case $m=3$.

Answer 3

Using the advice from @tired in the comments, we can write:

$$I_1(p)=\frac{2 \pi}{3 \sqrt{3}} \sum_{k=0}^\infty \frac{1}{k!^2} \left(\frac{1}{2}\right)_k \left(\frac{2}{3}\right)_k (1-p)^k=$$

$$=\frac{2 \pi}{3 \sqrt{3}} \sum_{k=0}^\infty \frac{1}{(1)_k} \left(\frac{1}{2}\right)_k \left(\frac{2}{3}\right)_k \frac{(1-p)^k}{k!}=\frac{2 \pi}{3 \sqrt{3}} {_2F_1} \left(\frac{1}{2},\frac{2}{3};1;1-p \right)$$

So this is just the usual Gauss hypergeometric function.

This answers my first question, but I'm hoping to get an answer to my second question as well.

---

If we speak of this integral as a mean, it's very close to both Arithmetic Geometric Mean and the Logarithmic Mean:

$$M(a,b)=\frac{a}{\sqrt{{_2F_1} \left(\frac{1}{2},\frac{2}{3};1;1-\frac{b^3}{a^3} \right)}}$$

$$a \geq b$$

I remind that the AGM can be written as:

$$\text{agm}(a,b)=\frac{a}{{_2F_1} \left(\frac{1}{2},\frac{1}{2};1;1-\frac{b^2}{a^2} \right)}$$

$$a \geq b$$

And numerically we have:

$$M(a,b) \leq \text{agm}(a,b)$$