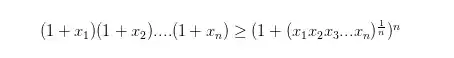Prove that $(1+a_1) \cdot (1+a_2) \cdot \dots \cdot (1+a_n) \geq 2^n$

Question

Let $a_1,a_2,\dots,a_n$ $\in$ $\mathbb{R}^+$ and $a_1\cdot a_2\cdots a_n=1$, , prove that $(1+a_1) \cdot (1+a_2) \cdot \dots \cdot (1+a_n) \geq 2^n$ I have tried factorising but it just lead me to extremily complicated equation that were extremily difficult to understand... Could someone help me?

Answer 1

applying the AM-GM inequality n-times we get $$(1+a_1)(1+a_2)\cdot...\cdot(1+a_n)\geq 2^n\sqrt{a_1a_2\cdot...\cdot a_n}=2^n$$ since $$a_1a_2\cdot...\cdot a_n=1$$

Answer 2

We will use basic AM-GM inequality to solve this problem.

Proof of the basic form

$$(\sqrt{a}-\sqrt{b})^2 \ge 0 \implies a + b -2\sqrt{ab} \ge 0 \implies {a+b\over2} \ge \sqrt{ab}$$

General proof here

---

Your question

$${1+a_1\over 2} \ge \sqrt{a_1} \implies \color{red}{1 + a_1} \ge \color{blue}{2\sqrt{a_1}}$$ $${1+a_2\over 2} \ge \sqrt{a_2} \implies \color{red}{1 + a_2} \ge \color{blue}{2\sqrt{a_2}}$$ $${1+a_3\over 2} \ge \sqrt{a_3} \implies \color{red}{1 + a_3} \ge \color{blue}{2\sqrt{a_3}}$$

$$\vdots$$

$${1+a_n\over 2} \ge \sqrt{a_n} \implies \color{red}{1 + a_n} \ge \color{blue}{2\sqrt{a_n}}$$

Multiplying all the red things together, $\color{red}{(1+a_1)(1+a_2)(1+a_3) \cdots (1+a_n)}$ .

And the blue things, $\color{blue}{(2\sqrt{a_1})(2\sqrt{a_2})(2\sqrt{a_3}) \cdots (2\sqrt{a_n})}= \color{blue}{2^n\sqrt{a_1a_2a_3\cdots a_n}} \leftarrow \text{(why ?)}$

Combing it all together we get,

$$\color{green}{(1+a_1)(1+a_2)\cdot...\cdot(1+a_n)\geq 2^n\sqrt{a_1a_2\cdot...\cdot a_n}}$$

$$\color{green}{(1+a_1)(1+a_2)\cdot...\cdot(1+a_n)\geq 2^n} \leftarrow \text{(why ?)}$$ $$\color{red}{\star}\color{green}{\star}\color{blue}{\star}\color{yellow}{\star}\color{indigo}{\star}\color{red}{\star}\color{green}{\star}\color{blue}{\star}\color{yellow}{\star}\color{indigo}{\star}\color{red}{\star}\color{green}{\star}\color{blue}{\star}\color{yellow}{\star}\color{indigo}{\star}\color{red}{\star}\color{green}{\star}\color{blue}{\star}\color{yellow}{\star}\color{indigo}{\star}$$ And we are done. If still something isn't clear please ask me.

---

Not very beginner friendly but certainly a good read on inequalities

Answer 3

See HUYGEN’S INEQUALITY. It's a more general result.

Answer 4

It's also Holder inequality for $n$ sequences.