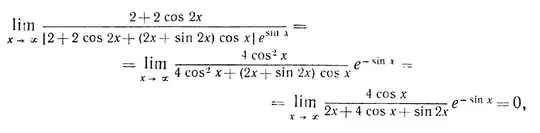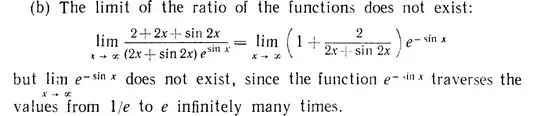Consider the following limit:$$\lim_{x \to\infty}\frac{2+2x+\sin(2x)}{(2x+\sin(2x))e^{\sin(x)}}$$
If we apply L'hospital's rule then we get:
Since the function $e^{-\sin(x)}$ is bounded and $\frac{4\cos(x)}{2x+4\cos(x)+\sin(2x)}e^{-\sin(x)}$ tends to $0$.
However, it is also stated that:
Furthermore, (referring to the application of the L'hospital's Rule) it is stated in conclusion that:
Since
$$-1 \leq -\sin x \leq 1, \ \ \ 1/e\leq e^{-\sin x}\leq e$$
Thus,
$$\frac{4\cos{x}}{2x+4\cos{x}+\sin{2x}}\cdot\frac{1}{e}\leq \frac{4\cos{x}}{2x+4\cos{x}+\sin{2x}}e^{-\sin{x}}\leq\frac{4\cos{x}}{2x+4\cos{x}+\sin{2x}}e$$
We know that $$\lim_{x\to\infty}\frac{4\cos{x}}{2x+4\cos{x}+\sin{2x}}=0$$
Thus by Squeeze Theorem, $$\lim_{x\to\infty}\frac{4\cos{x}}{2x+4\cos{x}+\sin{2x}}e^{-\sin{x}}=0$$
Nonexistence of the limit of $e^{-\sin{x}}$ does not imply that the limit of the whole expression doesn't exist.
For instance, limit of $(-1)^n$ as $n$ goes to $\infty$ does not exist. But, limit of $\frac{(-1)^n}{n}$ does exist, and it is equal to $0$, which can also be proven by using the Squeeze Theorem.
There seems to be nothing wrong with the original question.
EDIT After reading the edited post, I was very surprised to find an example where L'Hopital's rule doesn't really seem to work! I looked up on Wikipedia, and it states that the derivative of the denominator must not be zero.
I guess this is not a counterexample, just that L'Hopital's rule cannot be applied here.
The proof of Hôpital's rule rests on the following form of the mean value theorem: If $f$ and $g$ both are continuous on $[a,b]$ and differentiable in the interior $\ ]a,b[\ $, and if $g'(t)\ne0$ for all $t\in\ ]a,b[\ $, then there is a $\tau\in\ ]a,b[\ $ such that $${f(b)-f(a)\over g(b)-g(a)}={f'(\tau)\over g'(\tau)}\ .$$ The essential "technical assumption" $g'(t)\ne0$ is violated in the example at hand.
It would be nice to have a simpler example where it becomes intuitively clear why things can go wrong in such a case.
First of all +1 for coming up with an example which seems to violate the L'Hospital's Rule. However note that if $f(x)/g(x)$ is the original expression then $$\frac{f'(x)}{g'(x)} = \frac{4\cos^{2}x}{4\cos^{2}x + (2x + \sin 2x)\cos x}\cdot e^{-\sin x}$$ The problem now is that the limit of $f'(x)/g'(x)$ does not exist as $x \to \infty$ because the function $f'(x)/g'(x)$ is not defined in any interval of type $(a, \infty)$ precisely because the denominator $g'(x)$ vanishes for $x = (2n + 1)\pi/2$ for all $n \in \mathbb{Z}$.
As I have mentioned elsewhere on MSE it is important to understand the conditions under which L'Hospital's Rule is applicable. We must ensure that the ratio $f'(x)/g'(x)$ tends to a limit (or diverges to $\pm\infty$) and only then we can conclude the same behavior for ratio $f(x)/g(x)$. Apart from this we need the ratio $f(x)/g(x)$ to be one of the indeterminate forms "$0/0$" and "$\text{anything}/\pm\infty$".
