Taken from Wikipedia:
The number $e$ is the limit $$e = \lim_{n \to \infty} \left (1 + \frac{1}{n} \right)^n$$
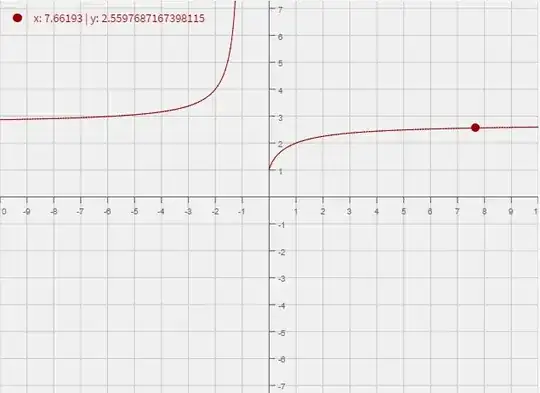
Graph of $f(x) = \left (1 + \dfrac{1}{x} \right)^x$ taken from here.
Its evident from the graph that the limit actually approaches $e$ as $x$ approaches $\infty$. So I tried approaching the value algebraically. My attempt:
$$\lim_{n \to \infty} \left (1 + \frac{1}{n} \right)^n$$ $$= \lim_{n \to \infty} \left(\frac{n + 1}{n}\right)^n$$ $$= \left(\lim_{n \to \infty} \left(\frac{n + 1}{n}\right) \right)^n$$ $$= 1^\infty$$
which is an indeterminate form. I cannot think of any other algebraic manipulation. My question is that how can I solve this limit algebraically?