Mick, the Op commented, "Your prediction must be false Sheldon. Notice that if in the interval [0,t] for any t>0 it is ordered then by induction it is ordered in [t,oo]....
Mick was seeking to change from the 1/2 iterate of $\exp_a;\;\exp_b$ which are not ordered as x gets arbitrarliy large, to using the half iterates of $\text{2sinh}_a;\;\text{2sinh}_b$ which Mick thought would be ordered. That doesn't match my results. Define $S_e$ as the superfunction for 2sinh for base e, $\text{2sinh}_e(z)=e^z-e^{-z}$,
and define $S_2$ as the superfunction for 2sinh for base 2, $\text{2sinh}_2(z)=2^z-2^{-z}$. These half iterates are generated from the fixed of zero by from the Koenig's method, using the Schröder equation to generate the two analytic superfunctions below:
$$S_e(z) = \text{2sinh}_e^{[z]}\;\;\;S_2(z) = \text{2sinh}_2^{[z]}$$
$$S_e(z+1) = \text{2sinh}_e(S_e(z));\;\;\;S_2(z+1) = \text{2sinh}_2(S_2(z))$$
Exactly analogous to before, consider the function
$$g(x) = S^{-1}_2(S_e(x+0.5))-S^{-1}_2(S_e(x))-0.5$$
if $g(x)=0\;$ then $\;\text{2sinh}_e^{0.5}(S_e(x))=\text{2sinh}_2^{0.5}(S_e(x))\;\;$ since $\;\text{2sinh}_2^{0.5}(S_e(x))=S_e(z+0.5)\;$ so we are comparing the half iterate base 2 with the half iterate base e.
$g(x)$ applies for base_2 and base_e, but any bases can work. The op hopes that $\forall x; \; \text{2sinh}_e^{0.5}(x)>\text{2sinh}_2^{0.5}(x)$, which would imply $\forall\; x\; g(x)>0$, but computationally as $x \to \infty, g(x)$ spends half of its time positive and half of its time negative. If x is large enough, when can easily show that $g(x+1) \approx g(x)$ and $g(x+0.5) \approx -g(x)$, where the approximation gets arbitrarily good as x increases.
First we show, x is large enough,
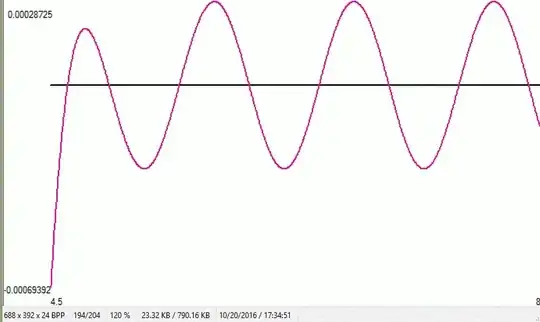
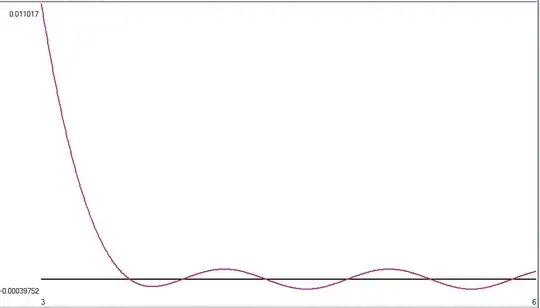
$S^{-1}_2(S_e(x+1)) \approx S^{-1}_2(S_e(x))+1$, then we show that if x is large enough $g(x+0.5)=-g(x)$. Therefore, unless $g(x)$ goes to $0+\epsilon\;\forall\; x$ as $x\to \infty$, g(x) will spend half of its time positive and half of its time negative. One can write a $\text{basechange}S_2(x)$ like equations as the limit of $\text{2sinh}_2^{[-n]}(S_e(x+n))$, which I conjecture would be the only solution (except for a constant) for $g(x)$ to go to $0+\epsilon \; \forall\;x$ as $x\to\infty\;$. Basechange type equations converge beautifully at the real axis, but they don't converge in any size radius in the conmplex plane; so the basechange is conjectured $C_\infty$ nowhere analytic. That is why I expected that the $\text{basechangeS}_2(x) \ne S_2(x)$ since we know $S_2(z)$ is analytic. And therefore, I wouldn't expect $g(x)$ to go to $0+\epsilon\;\forall\;x$ as $x \to \infty$. Computations agree. The first "zero" crossing corresponds to x=8.92760980698518338019E59, for which $\text{2sinh}^{0.5}_e(x)=\text{2sinh}^{0.5}_2(x).$ And once again from the graph below: $$\lim_{x \to \infty} g(x) \ne 0 \;\forall x$$
This is a graph of $g(x)$ with x ranging from 3..6, showing the 50% duty cycle as gets arbitrarily large.
For the remaining steps, we assume without being rigorous, that if x is large enough then $\text{2sinh}_e(x) \approx e^x\;$ and likewise for $\text{2sinh}_2(x)=2^x$, and then $\epsilon$ is insignificantly small in the equations below, provided $S_e(x-1)$ is large enough. Then following the same steps as in hte earlier answer, one can conclude:
$$S^{-1}_2(S_e(x+1)) = S^{-1}_2\left(\frac{S_e(x-1)}{\ln(2)} -\ln(\ln(2)) +\epsilon\right)+2$$
If x is large enough, then $S_e(x-1)$ is large enough to make the ln(ln(2)) term completely insignificant, and that $\epsilon$ is even more insignificant.
Continuing on as before, with a little bit of algebra $g(x+1) = g(x)+O\frac{1}{S_e(x-1)}$ where g(x+1) approaches g(x) as z increases. With a little bit algebra, we can also show that $g(x+0.5)=-g(x) + O\frac{1}{S_e(z-1)}\;$ therefore if $g(x)=0\;\;g(x+0.5)\;$ also approaches zero as x increases.