Combinatorial proof of $\sum_{1\le i\le n,\ 1\le j\le n}\min(i,j)=\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}6$

Question

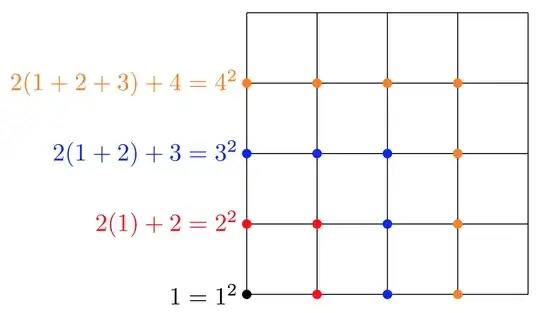
$$\sum_{1\le i\le n,\ 1\le j\le n}\min(i,j)=\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}6$$ Is there a link, if any, between these two identical sums?

It seems that there are two questions - one in the title and one in the body of the question. I would personally find it easier to answer if there were only one. — user259242, Oct 22 '16 at 11:47
@user259242: The title question is merely a more specific version of the one in the body. — Brian M. Scott, Oct 22 '16 at 11:48
@BrianM.Scott The one is asking about a combinatorial proof, the other about a 'link, if any'. These are different questions I suppose. In fact now that I'm reading over it, the second one seems trivial seeing that the quanties being equal provides the obvious link. — user259242, Oct 22 '16 at 11:52
@user259242: You should always read the question as a whole, including the title. In this case the title specifies the general kind of link desired. It’s also a good idea to give the OP some credit: ‘Yes, they’re equal’ is obviously not the kind of answer sought here. — Brian M. Scott, Oct 22 '16 at 12:03
See also: A combinatorial proof for the identity $\sum_i \sum_j \min(i,j) = \sum_k k^2$ — Martin Sleziak, Jun 24 '19 at 14:57

score 7 · Accepted Answer · answered Oct 22 '16 at 11:58

Look at an $n\times n$ array whose entry in row $i$ and column $j$ is $\min\{i,j\}$:

$$\begin{array}{ccc} 1&1&1&1&\ldots&1\\ 1&2&2&2&\ldots&2\\ 1&2&3&3&\ldots&3\\ 1&2&3&4&\ldots&4\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ 1&2&3&4&\ldots&n \end{array}$$

The entries in the first column and top row are $1$. If you strip those off, the entries in the first column and top row of what remains are $2$. If you strip those off, the entries in the first column and top row of what remains are $3$, and so on.

Now think of this as representing a top view of three-dimensional object made of $1\times1\times 1$ blocks in which the number in a cell represents the height of the object at that point; the object is a sort of stepped pyramid that reaches a height of $n$ in the lower righthand corner. The bottom layer contains $n^2$ blocks. The second layer contains $(n-1)^2$. And in general the $k$-th layer contains $(n+1-k)^2$ blocks, so the total number of blocks (and hence the sum of the entries in the array) is

$$\sum_{k=1}^n(n+1-k)^2=\sum_{k=1}^nk^2\;.$$

Nice explanation! (+1). – Hypergeometricx Oct 22 '16 at 15:03 — Hypergeometricx, Oct 22 '16 at 15:03

score 1 · Answer 2 · answered Oct 22 '16 at 11:55

I am not sure if this is the correct interpretation of the question, but assuming that the OP wants a proof of the equality for the identity, here is a proof. Note that $$\sum_{1\le i\le n,\ 1\le j\le n}\min(i,j)=\sum_{i=1}^n \sum_{j=1}^{i}\min(i,j)+\sum_{i=1}^n \sum_{j=i+1}^{n}\min(i,j)\\=\sum_{i=1}^n\sum_{j=1}^{i}j+\sum_{i=1}^n \sum_{j=i+1}^{n}i\\=\sum_{i=1}^n \frac{i(i+1)}{2}+\sum_{i=1}^n i(n-i)\\=\left(n+\frac{1}{2}\right)\frac{n(n+1)}{2}-\frac{n(n+1)(2n+1)}{12}\\=\frac{n(n+1)(2n+1)}{6}=\sum_{i=1}^ni^2 $$

score 1 · Answer 3 · answered Oct 22 '16 at 11:55

1

Not sure if this is what you are looking for:

answered Oct 22 '16 at 11:55

user246336

3,579

score 0 · Answer 4 · answered Oct 22 '16 at 12:00

For the second equality, notice that $\frac{n(n+1)(2n+1)}6=\binom{n+1}{2} + 2 \binom{n+1}{3}$. Both sides count the number of ordered triples $(i,j,k)(i,j,k)$ with $0≤i,j<k≤n$.
For a given $k$ there are $k^2$ ways to chose $i$ and $j$ in $\{0, 1, \ldots, k-1\}$. It is the left side.
Consider the cases $i=j$ and $i \neq j$ separately. If $i = j$, then there are $\binom{n+1}{2}$ such triples. We two numbers from $\{0, \ldots, n\}$; the smaller must be the value of $i$ and $j$ and the larger must be the value of $k$. If $i \neq j$, then there are $2\binom{n+1}{3}$ such triples, as we could have $i < j$ or $j < i$ for the smaller two numbers.
Thus $\sum_{i=1}^ni^2=\binom{n+1}{2} + 2 \binom{n+1}{3}=\frac{n(n+1)(2n+1)}6$

For the first equality (using the second one): $$\sum_{1\le i\le n,\ 1\le j\le n}\min(i,j)=\sum_{1\le i\le n}(\sum_{\ 1\le j\le i-1}\min(i,j)+\sum_{\ i\le j\le n}\min(i,j))=\sum_{1\le i\le n}(\sum_{\ 1\le j\le i-1}j+\sum_{\ i\le j\le n}i)=\sum_{1\le i\le n}(\frac{i(i-1)}{2}+i(n-i+1))=\sum_{1\le i\le n}\frac{i^2-i+2in-2i^2+2i}{2}\\=\sum_{1\le i\le n}\frac{-i^2+(2n+1)i}{2}=-\frac{1}{2}\sum_{i=1}^ni^2+\frac{2n+1}{2}\frac{n(n+1)}{2}\\=-\frac{1}{2}\sum_{i=1}^ni^2+\frac{3}{2}\frac{n(n+1)(2n+1)}6=\sum_{i=1}^ni^2$$

score 0 · Answer 5 · answered Oct 22 '16 at 15:02

$$\begin{array}{rr|rrrrrrr} \hline \min(i,j)&&i\\ &&1&2&3&4&\cdots &(n-2)&(n-1)&n\\ \hline j&1&1&1&1&1&\cdots &1&1&1\\ &2&1&2&2&2&\cdots &2&2&2\\ &3&1&2&3&3&\cdots &3&3&3\\ &4&1&2&3&4&\cdots &4&4&4\\ &\vdots&&&&&\ddots \\ &\vdots \\ &\vdots \\ &(n-2)&1&2&3&4&&\color{green}{(n-2)}&\color{green}{(n-2)}&\color{green}{(n-2)}\\ &(n-1)&1&2&3&4&&\color{green}{(n-2)}&\color{blue}{(n-1)}&\color{blue}{(n-1)}\\ &n&1&2&3&4&&\color{green}{(n-2)}&\color{blue}{(n-1)}&\color{red}n\\ \hline \end{array}$$

From the table above it is clear that $$\begin{align} \sum_{1\le i,j\le n}\min(i,j) &=\color{red}{1\cdot n}+\color{blue}{3\cdot (n-1)}+\color{green}{5\cdot (n-2)}+\cdots+(2n-1)\cdot 1 \\ &=\sum_{r=1}^n (2r-1)\color{orange}{(n+1-r)}\\ &=\sum_{r=1}^n \color{orange}{\sum_{i=r}^n}(2r-1)\\ &=\sum_{i=1}^n\sum_{r=1}^i (2r-1) \color{lightgrey}{=\sum_{i=1}^n\sum_{r=1}^i r^2-(r-1)^2}\\ &=\sum_{i=1}^n i^2\quad\blacksquare\\ \end{align}$$

Combinatorial proof of $\sum_{1\le i\le n,\ 1\le j\le n}\min(i,j)=\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}6$

5 Answers5

Linked