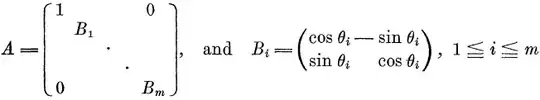similar transformation of rotation matrix by orthogonal matrix

Asked Nov 05 '16 at 01:10

Active Nov 05 '16 at 01:29

Viewed 422 times

I am reading an old paper by Horn (see ch.4):
https://www.jstor.org/stable/2372705?seq=1#page_scan_tab_contents

And for learning convenience of users, the following is a similar discussing:
Finding the Similarity Transform of a rotation matrix

Let $R$ be a rotation matrix.

Then there exists an orthogonal matrix $U$, such that $R = U^TAU$ with

So, for example, if $n=3$, then $A$ should look like
$$A = \begin{bmatrix}1 & 0& 0 \\0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}$$

How to prove this? (WLOG, suppose the size of matrices is odd.) In fact, $A$ is also an rotation matrix.

edited Apr 13 '17 at 12:21

Community

asked Nov 05 '16 at 01:10

sleeve chen

8,281

1

it is just the real version of the spectral theorem. Each $B_i$ corresponds to a complex conjugated pair eigenvalues of $R$. – user251257 Nov 05 '16 at 02:29
@user251257 I see, thanks. The dimension of $B_i$ in such representation still makes me feel odd however. – sleeve chen Nov 05 '16 at 02:34
what do you mean? – user251257 Nov 05 '16 at 02:39
@user251257 I mean I am not used to the eigenvalue $e^{\pm \theta} \in R$ corresponds to the eigenvalue $B_i\in R^{2\times 2}$ – sleeve chen Nov 05 '16 at 02:46
1

$B_i$ itself is a rotation, so it's eigenvalues have the form $\exp(\pm \mathbf i \beta)$ where $\mathbf i$ is the imaginary unit and $\beta\in [0,2\pi)$. – user251257 Nov 05 '16 at 02:50

similar transformation of rotation matrix by orthogonal matrix

0 Answers0