The process used by Archimedes is a very clever trick. We don not know how to calculate the area of a figure with a curvy side like that one. On the other hand, we are quite good at calculating the area of shapes like squares, triangles and rectangles. Now what if:
Instead of trying to directly calculate the area of the shape defined by the curve, we tried to calculate the area of something we know has always smaller area and the area of something that has always a greater area, and then squeeze them both to get the area of the parabola.
That is, imagine there is some shape $S_+$ for which you know the area. You also know that by altering slightly the shape $S_+$, you can reduce its total area while still having greater area than the parabola.
Conversely, imagine there is some shape $S_-$ for which you know the area and that by altering that shape $S_-$ you can make its area increase, while still having smaller area than the parabola. Now let's call $A$ the area of the parabola.
From the way we built $S_-$ and $S_+$ we know that $A > S_-$ and $A < S_+$ therefore $S_- < A < S_+$. If you push the area of $S_+$ down and you pull the area of $S_-$ up, you get a smaller range where $A$ could lie. Now imagine you could make $S_-$ as close to $S_+$ as you wanted! Then you could squeeze $A$ between $S_-$ and $S_+$ which would be soooo close you could almost assume $S_- = A = S_+$.
This makes some sense right? Now what shapes should you choose for $S_-$ and $S_+$? Well, lets build a not-that-simple shape that is composed of super simple shapes: rectangles! We let $S_-$ be the shape whose area is in green in the image and we let $S_+$ be the shape whose area is in red in the image.
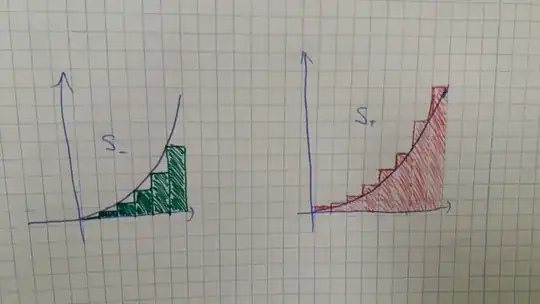
So imagine we want to measure the area $A$ in squares. We can see that $S_-$ is made up of several rectangles with width $1 sq$ and different heights. So total area of $S_-$ is $\sum {A}_{rect} = \sum width \times height_{rect} = width * \sum height_{rect}$. And in a similar fashion for $S_+$.
Now I will ask you to do the following: grab a piece of paper and mimic my drawing, but instead of using rectangles with width of 1 square, draw them with width $1/2$ square. Look at your drawings and try to understand that your $S_-$ will be bigger than mine, because the rectangles will be closer to the line of the parabola from below and that the area of your $S_+$ will be smaller than mine, for the same reason: the red rectangles are closer to the parabola line.
If you could draw rectangles with width infinitely small, both approximations would be very, very close and you would arrive at the formula that Archimedes arrived. The area below the parabola is $\frac{b^3}{3}$
Let's dig a bit more why that is. Imagine you want to calculate the area below the parabola that starts with $x=0$ and goes up until $x=b$. The best way you have to tell me what shapes $S$ you are using is telling me how many rectangles you have. Because we have the same value of $b$, that suffices. So let's say you create $n$ rectangles all of equal width. Therefore you are splitting the interval $[0, b]$ in $n$ parts, each of length $b/n$. Now make a graph and tick the $xx$ axis to accordingly split the interval in those parts. Do this for two graphs. One for $S_-$ and the other for $S_+$. Now connect each tick to the parabola with a vertical line. Because $S_-$ has area below the parabola, connect each vertical line to the one on the right, to create a rectangle below the parabola. For $S_+$, connect each vertical line with the one on the left creating a rectangle above the parabola.
(Note that you have $n$ rectangles on both graphs. Notice that the ith rectangle spans from $x = \frac{(i-1)b}{n}$ to $x = \frac{ib}{n}$ and therefore the height of the ith rectangle is either $(\frac{(i-1)b}{n})^2$ or $(\frac{ib}{n})^2$ depending on the shape you are talking about.
Now all we have to do is calculate the are of $S_-$ and $S_+$. Let's start with $S_-$. To follow along, and whenever you get lost, refer to your drawing!
$$S_- = \sum_{i=0}^{n-1} \left(\frac{b}{n}\right) \cdot \left(\frac{ib}{n}\right)^2 = \left(\frac{b}{n}\right) \cdot \sum_{i=0}^{n-1} \left(\frac{b}{n}\right)^2 \cdot i^2 = \left(\frac{b}{n}\right)^3 \cdot \sum_{i=0}^{n-1} i^2$$
Which is exactly what you have. In a similar fashion we can compute $S_+$. The only change is in the indices of the summation:
$$S_+ = \sum_{i=1}^{n} \left(\frac{b}{n}\right) \cdot \left(\frac{ib}{n}\right)^2 = \left(\frac{b}{n}\right) \cdot \sum_{i=1}^{n} \left(\frac{b}{n}\right)^2 \cdot i^2 = \left(\frac{b}{n}\right)^3 \cdot \sum_{i=1}^{n} i^2$$
Which again is the same as you have. Now if you derive it/know it/google it you get that the summation of the first $n$ squares is
$$\left(\sum_{i=0}^{n} = \right) \sum_{i=1}^{n} = \frac{n(n+1)(2n+1)}{6}$$
Substituting above we get, for $S_-$ and for $S_+$
$$S_- = \left(\frac{b}{n}\right)^3 \cdot \frac{(n-1)n(2n-1)}{6}$$
$$S_+ = \left(\frac{b}{n}\right)^3 \cdot \frac{n(n+1)(2n+1)}{6}$$
If you take the limit $\lim{n \rightarrow \infty}$ you get
$$S_- = S_+ = \frac{b^3}{3}$$
