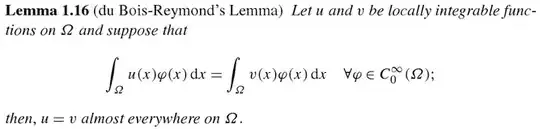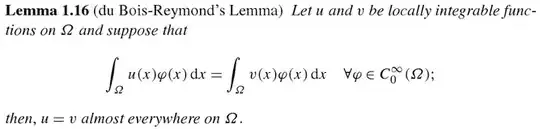0

Let

  • $d\in\mathbb N$
  • $\lambda$ denote the Lebesgue measure on $\mathbb R^d$
  • $\Lambda\subseteq\mathbb R^d$ be open
  • $u\in H^2(\Lambda)$
  • $f\in L^2(\Lambda)$

Assume $$-\Delta u=f\tag 1$$ in the sense of distributions. Why can we conclude that $$\int_\Lambda(-\Delta u)v\:{\rm d}\lambda=\int_\Lambda fv\:{\rm d}\lambda\tag 2$$ for all $v\in H^1(\Lambda)$.

I've read that in a lecture note (see page 78) and don't understand this. Clearly, the claim would be true for $v\in H_0^1(\Lambda)$. Maybe they use an approximation argument that I'm not aware of (with that in mind, please feel free to add any regularity assumption on $\Lambda$).

0xbadf00d
  • 13,422

1 Answers1

1

This comes from the regularity of $u$. For $u\in H^2$, $$-\Delta u=f\quad\text{in}\quad\mathcal{D}'(\Lambda)\tag{#}$$ means $$\int_\Lambda(-\Delta u)\varphi\;\mathrm{d}\lambda=\int_\Lambda f\varphi\;\mathrm{d}\lambda\quad\forall\ \varphi\in\mathcal{D}(\Lambda)$$ which implies $$-\Delta u=f\quad\text{a.e.}\tag{$*$}$$ by the du Bois-Reymond Lemma. Multiplying $(*)$ by $v\in H^1(\Lambda)$ and integrating over $\Lambda$ you get the result (without any further regularity on $\Lambda$).

Edit

Let $\Lambda\subset\mathbb{R}^d$ be open and $f,u\in L^1 _{\text{loc}}(\Lambda)$. The distributions $f$, $u$ and $\Delta u$ are defined by $$\langle f,\varphi\rangle=\int_\Lambda f\varphi\;\mathrm{d}\lambda,\quad \langle u,\varphi\rangle=\int_\Lambda u\varphi\;\mathrm{d}\lambda,\quad \langle\Delta u,\varphi\rangle=\langle u,\Delta\varphi\rangle=\int_\Lambda u\Delta \varphi\;\mathrm{d}\lambda,\quad\varphi\in\mathcal{D}(\Lambda).$$ Assume that $u,f\in L^1_{\text{loc}}(\Lambda)$ and $-\Delta u=f$ in $\mathcal{D}'(\Lambda)$. Then $$-\int_\Lambda u\Delta \varphi\;\mathrm{d}\lambda=\int_\Lambda f \varphi\;\mathrm{d}\lambda.$$

If, additionally, $u\in H^2(\Lambda)$ and $\Lambda$ is bounded with Lipschitz boundary, then (Corollary 3.46 here) $$\int_\Lambda (-\Delta u) \varphi\;\mathrm{d}\lambda=-\int_\Lambda u\Delta \varphi\;\mathrm{d}\lambda=\int_\Lambda f \varphi\;\mathrm{d}\lambda.$$ Therefore by the Du Bois Reymond Lemma (Lema 1.16 here) $$-\Delta u=f\quad\text{a.e.}$$

Conclusion: $(\#)$ implies that $$\int_\Lambda(-\Delta u)v\;\mathrm{d}\lambda=\int_\Lambda fv$$ for all $v\in H^1(\Lambda)$ provided that $\Lambda$ is a bounded open set with Lipschitz boundary and $u\in H^2(\Lambda)$.

Edit 2

Print of the third link:

enter image description here

Pedro
  • 18,817
  • 7
  • 65
  • 127
  • So, your statement is true for any open $\Lambda$? Or do we need boundedness too? 2. For $(\ast)$, it's sufficient that $u$ has a weak Laplacian $\Delta u\in L_{\text{loc}}^1(\Lambda)$. So, the statement should be true for more general $u$ which don't necessarily belong to $H^2(\Lambda)$. Is it true for even more general $u$?
    • – 0xbadf00d Dec 21 '16 at 19:19
  • Or do you exploit $H^2(\Lambda)\subseteq C^0(\overline\Lambda)$? I guess you do that in the invocation of the Lemma? In that case, the statement is true only when $d<4$. – 0xbadf00d Dec 21 '16 at 19:31
  • 1
    @0xbadf00d We need $u$ and $\Lambda$ regular enough so that we can apply integration by parts and the Du Bois Reymond Lemma. For the first, the basic assumptions are $u\in H^2(\Lambda)$ and $\Lambda$ bounded with Lipschitz boundary (see Corollary 3.46 here); for the second, the basic assumptions are $\Lambda$ open and $u$ locally integrable (see Lema 1.16 here). As the Du Bois-Reymond Lemma is very general, the key point is the needed assumptions for the integration by parts. See the edit in my answer. No, I didn't exploit the said embedding. – Pedro Dec 21 '16 at 23:01
  • It should be $$\color{red}{-}\int_\Lambda u\Delta \varphi;\mathrm{d}\lambda=\int_\Lambda f \varphi;\mathrm{d}\lambda$$ in your second centered equation of your edit. – 0xbadf00d Dec 22 '16 at 13:33
  • Your link to Lemma 1.16 is not working. – 0xbadf00d Dec 22 '16 at 13:35
  • Suppose $p\in H^1(\Lambda)$ and $f\in L^2(\Lambda,\mathbb R^d)$ with $$\langle\nabla\phi,\nabla p\rangle_{L^2(\Lambda,:\mathbb R^d)}=\langle\nabla\phi,f\rangle_{L^2(\Lambda,:\mathbb R^d)};;;\text{for all }\phi\in C_c^\infty(\Lambda);.\tag 3$$ Can we conclude $\nabla p=f$ a.e. by the du Bois-Reymond Lemma too? – 0xbadf00d Dec 22 '16 at 13:45
  • @0xbadf00d I have corrected the signs and added a print of the link. – Pedro Dec 22 '16 at 15:51
  • @0xbadf00d For your last question, let us consider the case $d=1$. Then $(3)$ reduces to $$\langle\partial_x\phi,\partial_x p\rangle_{L^2(\Lambda,:\mathbb R^d)}=\langle\partial_x\phi,f\rangle_{L^2(\Lambda,:\mathbb R^d)};;\forall\ \phi\in C_c^\infty(\Lambda)$$ By this corollary of the Du Bois-Reymond Lemma we can conclude that there exists a consatnt $c$ (not necessarily zero) such that $\nabla p=f+c$ a.e. For $d>1$, is not clear for me what do you mean by $\langle\nabla \phi,f\rangle_{L^2(\Lambda,:\mathbb R^d)}$ and $\nabla p=f$. – Pedro Dec 22 '16 at 15:51
  • Why it's not clear for you what $\langle\nabla \phi,f\rangle_{L^2(\Lambda,:\mathbb R^d)}$ is? $\nabla\phi=(\partial_{x_1}\phi,\ldots,\partial_{x_d}\phi)^T$ is the gradient of $\phi$ and it's clear that it belongs to $L^2(\Lambda,\mathbb R^d)$. $\nabla p=f$ (in $L^2(\Lambda,\mathbb R^d)$) would perfectly make sense. – 0xbadf00d Dec 22 '16 at 16:41
  • Let me remark that this question is the reason for my last question here. I hope that I can show that the solution $p$ of $(3)$ (in the other question) satisfies $γ\nu\nabla p=γ\nu u$ which should be the case, if I could show that $\langle∇q,\nabla p\rangle_{L^2(Λ,:\mathbb R^d)}=\langle∇q, u\rangle_{L^2(Λ,:\mathbb R^d)}$ for all $q\in W$. EDIT: In the previous statement, I assume that the given $u\in L^2(Λ,\mathbb R^d)$ satisfies $\nabla\cdot u\in L^2(Λ)$. – 0xbadf00d Dec 22 '16 at 21:19