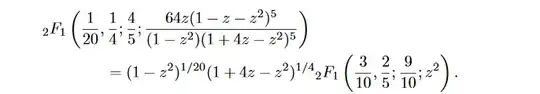On $_2F_1(\tfrac13,\tfrac23;\tfrac56;\tfrac{27}{32}) = \tfrac85$ and $_2F_1(\tfrac14,\tfrac34;\tfrac78;\tfrac{48}{49}) = \tfrac{\sqrt7}3(1+\sqrt2)$

Question

Consider the rather interesting and new evaluations for $_2F_1\left(\tfrac14,\tfrac34;\color{blue}{\tfrac{n}{n+1}};z\right)$,

$$\begin{aligned} _2F_1\left(\tfrac14,\tfrac34;\color{blue}{\tfrac23};\tfrac{2^2\times3^3}{121}\right) &= \large\tfrac{\sqrt{33}}{3}\\[2mm] _2F_1\left(\tfrac14,\tfrac34;\color{blue}{\tfrac56};-\tfrac{135}{121}\right) &=\large\tfrac{\sqrt{33}}{10^{5/6}}\\[2mm] _2F_1\left(\tfrac14,\tfrac34;\color{blue}{\tfrac78};\tfrac{48}{49}\right) &= \tfrac{\sqrt7}3(1+\sqrt2)\\[2mm] _2F_1\left(\tfrac14,\tfrac34;\color{blue}{\tfrac9{10}};\tfrac{4}{5}\right) &=\large \tfrac1{5^{1/4}}\,\phi^{3/2}\end{aligned}$$ and golden ratio $\phi$, with the last a transformed version of Nemo's answer. The transformation,

$$_2F_1\left(\tfrac14,\tfrac34;c;\tfrac{4z(z-1)}{(1-2z)^2}\right)=\sqrt{1-2z}\,(1-z)^{1-c}\,_2F_1\left(-c+\tfrac32,\,c-\tfrac12;c;z\right)$$ allows it to be transformed to another form also with $a+b=-c+\tfrac32+c-\tfrac12 =1$. For example, the second one yields, $$\,_2F_1\left(\tfrac13,\tfrac23;\color{blue}{\tfrac56};\tfrac{5}{32}\right) = \large\tfrac4{5^{5/6}}$$ which is related to the the known, $$\,_2F_1\left(\tfrac13,\tfrac23;\color{blue}{\tfrac56};\tfrac{27}{32}\right) = \tfrac85$$ However, only the first one is known to belong to an infinite family. The others apparently cannot be transformed to the group of families with $a+b = c$, nor to this group with $\,_2F_1\left(a,a;a+\tfrac12;z\right)$, and seem to be isolated results.

However, the "sensible" form of the $z$, i.e. note the squares and that $\tfrac{135}{121}+1=\big(\tfrac{16}{11}\big)^2$, may suggest the others also are just the smallest members of an infinite family of algebraic numbers.

P.S. Both the silver ratio $\sigma = 1+\sqrt2$ and golden ratio $\phi$ are fundamental units.

Questions:

1. Using transformations, can we in fact derive the three from any of the families in the linked posts?
2. What other examples are there of "isolated" results?

Answer 1

This is a partial answer to the 2nd question. It explains how to find "isolated" examples of hypergeometric functions that have algebraic values at algebraic points using educated guess combined with numerical experimentation. The following example comes from the transformation$\tag{1}$ taken from this article: $$ {}_2F_1\left(\frac{3}{10},\frac{2}{5};\frac{9}{10};\frac{1}{\phi ^2}\right)=\frac{\phi ^{9/5}}{\sqrt{5}}.\tag{2} $$ Suppose one evaluates the RHS of (1) at the point $z=1/\phi$ ($\phi-$ Golden ratio), where the argument of the hypergeometric function on the LHS of (1) vanishes due to $1-1/\phi-1/\phi^2=0$. One might expect that ${}_2F_1\left(\frac{3}{10},\frac{2}{5};\frac{9}{10};\frac{1}{\phi ^2}\right)$ equals $\frac{1}{\sqrt[20]{1-1/\phi^2}} \frac{1}{\sqrt[4]{1+4/ \phi-1/\phi^2}}$. However numerical evaluation shows that this is not the case, and this is due to the fact that $z=1/\phi$ does not belong to the validity range of (1). But this doesn't matter because one might easily find possible closed form (2) for ${}_2F_1\left(\frac{3}{10},\frac{2}{5};\frac{9}{10};\frac{1}{\phi ^2}\right)$ by numerical experimentation. After application of Euler transformation (2) takes the nice form $${}_2F_1\left(\frac{1}{2},\frac{3}{5};\frac{9}{10};\frac{1}{\phi ^2}\right)=\frac{\phi ^{2}}{\sqrt{5}},\tag{3}$$ where parameters of the hypergeometric function satisfy $c=1+a-b$.

I want to stress that (2) and (3) are only conjectures because this method doesn't provide the proof.

To obtain another algebraic value consider the transformation (22) in the article https://arxiv.org/abs/0807.4808 $$ \, _2F_1\left(a,\frac{2 a+1}{6};\frac{1}{2};x\right)=\left(\frac{x}{3}+1\right)^{-a}\, _2F_1\left(\frac{a}{3},\frac{a+1}{3};\frac{1}{2};\frac{x (9-x)^2}{(x+3)^3}\right). $$ $x=9$ does not belong to validity range of (1) but one expects that ${}_2F_1\left(a,\frac{2 a+1}{6};\frac{1}{2};9\right)$ is algebraic and indeed according to DLMF 15.8.2 and DLMF 15.4.32 we have $$ {}_2F_1\left(a,\frac{2 a+1}{6};\frac{1}{2};9\right)=\frac{e^{-\pi i a} \cos \pi a-e^{-\pi i/6-\pi ia/3}\sin \pi a}{2^{2 a+1} \sin \left(\frac{\pi }{6}-\frac{2 \pi a}{3}\right)}. $$