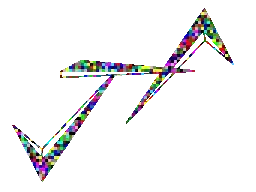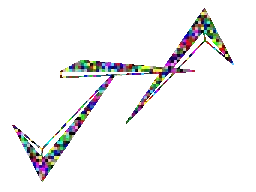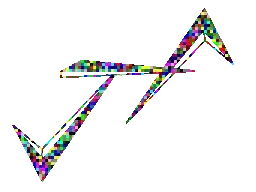5

Somewhat goofy question, not for any serious purpose, and I can't think of a really good title (please suggest better title/tags).

I'm adding rotation functionality to my animated gif generation program, and noticed the following behaviors that suggested the question formulated below. For reference, origin is at the center of each image, positive-$x$-axis is to your right, positive-$y$ is up, and positive-$z$ is poking you in the eye (as per right-hand screw rule). And the reference image I'm using is just my "jf" logo.

Now, the following image is initially flat/two-dimensional in the $x,y$-plane, and we're rotating it about the $y$-axis, call the axis of rotation $u=(0,1,0)$,...

enter image description here

But is it rotating clockwise or counterclockwise??? That's a typical optical illusion, which you may have already seen with a spinning ballerina. Your brain can see it spinning one way for a while, and then see it spinning the other way.

On the other hand, when $u=(0,0,1)$ rotating around the $z$-axis, it's unambiguously spinning clockwise, as follows...

enter image description here

There's no way you can "see" anything else. But if we now take $u=(1,1,1)$, normalizing $u$, we see...

enter image description here

And with a little effort, that can be seen rotating several ways as well. So here's the question...

...that parameter space $u=(x,y,z)$ describing the axis of rotation is continuous. But the "multistable-optical-illusion-boundary", when you can/can't see the same image appearing to rotate differently, must be a discrete step-function kind of thing. So where's that boundary???, i.e., what's the $(x,y,z)$-subspace of $u$ where you can/can't see this kind of illusion? (note: since $u$ is normalized, its space is really the two-dimensional surface of the three-dimensional unit sphere)

John Forkosh
  • 712
  • 1
    These values you described are more likely to be qualitative. I doubt that they could ever be quantized. – polfosol Dec 30 '16 at 09:54
  • 1
    I like this question very much - though it may lead to psychological rather than mathematical investigations. Purely mathematically, rotation in parallel perspective about $(x,y,z)$ is indistinguishable from rotation about $(x,y,-z)$ and that's different for all cases except $(0,0,\pm1)$ – Hagen von Eitzen Dec 30 '16 at 09:55

2 Answers2

2

Since there is no depth perception in these images (for which proper perspective instead of parallel perspective might suffice), the flat image does not change if we reflect the 3d situation at the $xy$ plane (and up to translation, this reflection is the only ambiguity). Such a reflection turns a rotation around $(x,y,z)$ into a negative rotation around $(x,y,-z)$, i.e., into a rotation around $(-x,-y,z)$. Therefore, the two possible interpretations coincide (i.e., there is only one interpretation) iff $x=y=0$. So in effect there is no weird transition that breaks some continuity somewhere, but instead the two interpretations just happen to coincide for the straight-to-the-face-axis case. For a just barely tilted axis, we ought to have the illusion with just slightly differing axes. So the real question might be: For what angle between $(x,y,z)$ and $(-x,-y,z)$ can we perceive a difference?

Hagen von Eitzen
  • 374,180
0

This is a follow-up/comment to Hagen's answer, but I can't post <img>'s in a comment. And I'm not entirely sure whether or not what I'm saying is just another way of saying what Hagen said...

I think the answer (which may be equivalent to Hagen's) is what's called a "splice point", which is when a 2-D image rotating about an axis in 3-space goes through an angle where it presents a straight line to the viewer, like this...

enter image description here

So any image that rotates through a splice point can be imagined to "come out the other side", so to speak, rotating the other way. Otherwise, without a splice point, the direction of rotation will be unambiguous to the eye. And, as in the example, "splice points" are typically used to change content "seamlessly", which is what suggested to me that it also answers the question here.

John Forkosh
  • 712