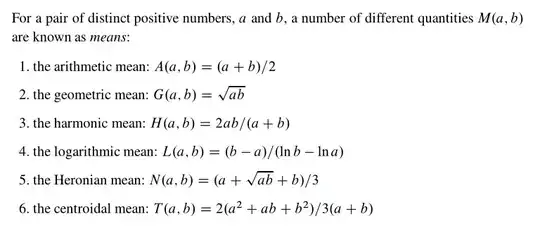14

I took calculus courses and have read some books about it. Most of them is similar: There are the definitions and some applications but not enough depth. For example, it is very common to find the problem of the box in calculus books:

Having a sheet of paper of area $a^2$, how can we fold it into a box in a way that maximizes the volume?

This is a really interesting problem and I guess that the books could have a little bit more about it, in a way that almost suggests the study of optimization problems. The problem for me is that calculus by itself doesn't seems stimulating enough. But I have found several titles that make calculus more interesting. Take a look at this result from Chen's: Excursions in Classical Analysis.

enter image description here

enter image description here

I think this is a very interesting and elegant result! One can have all these means as a function based on simple integrals and as a bonus, you also gain a very easy way to deduce inequalities between all them! I have also found

Moll's books are filled with the study of polynomials, Riemann's $\zeta$ Function, Legendre polynomials, Chebyshev polynomials, Hermite polynomials, $\Gamma$ function, Logarithmic Integrals, etc.

Kazarinoff even makes an appeal in his book:

enter image description here

Gardiner's book is IMO an excellent choice to explain why we need a more rigorous analysis. Very soon in the book, he already presents some functions in which a naive usage of ideas in calculus can take one to hazardous consequences.

Shahriari's book is a real gem. Just take a look at its contents. It has a section on dynamical systems!

What I call "interesting" here is the suggestion of using calculus to discover neat problems both in analysis and in others areas of mathematics or a decent and organic explanation of the whys. I felt that calculus was no stimulating because the derivative is basically "a tool for finding lines tangent to functions" and the integral is basically "a tool for measuring the are under a curve", obviously: These are worthy, but where can we go from there? The question is, do you know more books that complement this list?

Behind the scenes: The original title of the question was: "Where to find books with interesting activities using calculus?" but MSE suggested a change for a better title. I changed to this and the warning disappeared: If there is no warning, then this is a better title! (Also, I watched this today.)

Community
  • 1
Red Banana
  • 23,956
  • 20
  • 91
  • 192
  • 2
    This question clearly took quite a bit of time to write out. It would be ideal if the down-voters would comment to give some indication as to how the OP could, in their eyes, improve matters. – Benjamin Dickman Jan 07 '17 at 06:44
  • 1
    I fully agree with what Kazarinoff says. The $\epsilon, \delta$ stuff is nothing more than an elementary exercise in inequalities and the crux of analysis lies in the real number system and not in the $ \epsilon, \delta$ gymnastics or the use of symbols like $\forall, \exists$ from logic. – Paramanand Singh Jan 07 '17 at 06:51
  • 1
    And I have to agree with your comment about downvotes. While I prefer not to go overboard like you on this matter, I believe most people on the receiving end of silent downvotes feel something similar. +1 for the references to excellent books. – Paramanand Singh Jan 07 '17 at 07:06
  • 1
    Really very interesting question and list! And über-funny title xDDD Ofc +1. – Masacroso Jan 07 '17 at 09:40
  • 1
    I'm still a fan of Spivak's Calculus, who brings in topics like non-differentiable functions, $\pi$ is irrational, $e$ is transcendental, and aims to "present calculus not merely as a prelude to but as the first real encounter with mathematics." – Trurl Jan 13 '17 at 13:38

1 Answers1

3

Here are three book recommendations which might get the attribute ''interesting'' in OPs sense.

Each of these books has analysis at the core but also invites the reader to look outside the box. They are sometimes rather challenging but many parts will be accessible and the other parts might invite the reader to do some further research for his own benefit.

The other two books have many subjects in common, are both focused at analysis and number theory, but provide completely different approaches. Both are IMO treasures of knowledge and fun.

  • Experimentation in Mathematics - Computational Paths to Discovery by J. Borwein, D. Bailey and R. Girgensohn

    You might have a look at the table of contents or the summary, but this is rather misleading as it does not give you a proper insight about the content. Since there are so many different nice things to discover, I suggest to take this book from somewhere and skim through it in order to get a first impression.

  • Euler Through Time - A New look at Old Themes by V.S. Varajarajan

    The intention of this book is not to cover all of Euler's work, but instead focus at important contributions to analysis and (analytic) number theory. The fascinating thing here is, the author does not stick at the past but instead examines his work and its relation to current mathematics.

Community
  • 1
Markus Scheuer
  • 108,315