Order of sublattice.

Question

I am reading serre's book A Course in Arithmetic"", and want to understand the Hecke operator. Let $\omega_1,\omega_2\in \mathbb{C},$ and $\frac{\omega_1}{\omega_1}\in \mathbb{H},$ where $\mathbb{H}$ stands for upper half plane, we define a lattice in $\mathbb{C}$ as follows: \begin{align*} \Gamma:=\mathbb{Z}\omega_1\oplus\mathbb{Z}\omega_2. \end{align*} It is obviously a additive subgroup of $\mathbb{C}$. Let $\mathcal{R}$ be the set of lattices of $\mathbb{C}$, and $X_\mathcal{R}$ be the free abelian group generated by $\mathcal{R}$.

Suppose that $T(n):X_\mathcal{R}\longrightarrow X_\mathcal{R}$ is a group homomorphism defined as follow: \begin{align*} T(n)\Gamma=\sum_{(\Gamma,\Gamma')=n}\Gamma'. \end{align*} In other words, $T(n)$ transforms a lattice to the sum of its sub-lattices of index $n$.

With the notations above, he said: 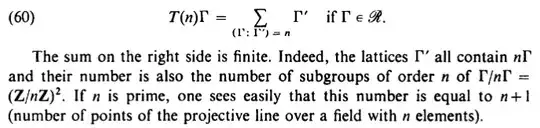My qusetion:

• why the lattice $\Gamma'$ must contains $n\Gamma$?
• why the number of $\Gamma'$ is equal to the number of subgroups of $(\mathbb{Z}/n\mathbb{Z})^2$ of order $n$?
• how can we count the number of projective lines over finite fields?

---

Some of ny ideas:

• I sence that it may need "Fundamental theorem on homomorphisms".

• I have known a obvious isomorphism $\mathbb{Z}\omega_1\oplus\mathbb{Z}\omega_2\cong\mathbb{Z}\times\mathbb{Z}.$ Thus we can just consider the subgroup of $\mathbb{Z}\times\mathbb{Z}$.

  Any help is greatly appreciated!

Answer 1

Note that as $\Gamma'$ has index $n$ in $\Gamma$, we have that $\Gamma/\Gamma'$ has order $n$ as an abelian group and so for every $\overline{x}\in \Gamma/\Gamma'$, $n\overline{x}=\overline{0}$. This just means that for every $x\in\Gamma$, $nx\in \Gamma'$. In other words, $$n\Gamma\subseteq \Gamma'\text{.}$$ Once this is clear, note that there is by the isomorphism (or correspondence) theorems (depending in your terminology) a one-to-one correspondence between subgroups of $\Gamma$ containing $n\Gamma$ and subgroups of $\Gamma/n\Gamma$ given by $$L\leq\Gamma\mapsto L/n\Gamma$$ that preserves the index of the subgroups (by the third isomorphism theorem). In this way, we have that there as many subgroups of index $n$ in $\Gamma$ as subgroups of index $n$ in $\Gamma/n\Gamma$ as every subgroup of index $n$ of $\Gamma$ contains $n\Gamma$.

As you notice, $\Gamma$ is isomorphic to $\mathbb{Z}\times \mathbb{Z}$. Hence $\Gamma/n\Gamma$ is isomorphic to $\mathbb{Z}\times \mathbb{Z}/n(\mathbb{Z}\times\mathbb{Z})$ which is just $(\mathbb{Z}/n\mathbb{Z})^2$. Hence there are as many subgroups of index $n$ in $\Gamma$ as subgroups of index $n$ in $(\mathbb{Z}/n\mathbb{Z})^2$ which, as $(\mathbb{Z}/n\mathbb{Z})^2$ has order $n^2$, are also the subgroups of order $n$ of $(\mathbb{Z}/n\mathbb{Z})^2$.

In conclusion, the essential ingredients in all these arguments have been Lagrange's index theorem for subgroups (and its corollaries) and the isomorphism $\Gamma\cong \mathbb{Z}\times\mathbb{Z}$.

For your last question, just notice that it is the same as counting the number of linear planes in a vector space over a finite field. You can found the answer to that question in general in the question "How to count number of bases and subspaces of a given dimension in a vector space over a finite field?". However, note that the subgroups of order $p$ of $(\mathbb{Z}/p\mathbb{Z})^2$ correspond to the points of the projective line over $\mathbb{Z}/p\mathbb{Z}$.