interpretation of SVD for text mining topic analysis

Question

Background

I'm learning about text mining by building my own text mining toolkit from scratch - the best way to learn!

SVD

The Singular Value Decomposition is often cited as a good way to:

1. Visualise high dimensional data (word-document matrix) in 2d/3d
2. Extract key topics by reducing dimensions

I've spent about a month learning about the SVD .. I must admit much of the online tutorials, papers, university lecture slides, .. and even proper printed textbooks are not that easy to digest.

Here's my understanding so far: SVD demystified (blog)

I think I have understood the following:

• Any (real) matrix can be decomposed uniquely into 3 multiplied matrices using SVD, $A = U \cdot S \cdot V^T$
• $S$ is a diagonal matrix of singular values, in descending order of magnitude
• $U$ and $V^T$ are matrices of orthonormal vectors

I understand that we can reduce the dimensions by filtering out less significant information by zero-ing the smaller elements of $S$, and reconstructing the original data. If I wanted to reduce dimensions to 2, I'd only keep the top 2 elements of $S$ .. the top-left-most elements of the diagonal $S$

My Problem

To see the documents projected onto the reduced dimension space, I've seen people use $S_{reduced} \cdot V^T$. Why? What's the interpretation of $S_{reduced} \cdot V^T$?

Similarly, to see the topics, I've seen people use $U \cdot S_{reduced}$. Why? What's the interpretation of this?

My limited school maths tells me I should look at these as transformations (rotation, scale) ... but that doesn't help clarify it either.

Answer 1

The topic of low rank approximation is sprinkled throughout Math SE:

Low-rank Approximation with SVD on a Kernel Matrix

Matrix values increasing after SVD, singular value decomposition

The singular value spectrum may span several orders of magnitude. It seems natural that the contributions from the larger values are more important. Numerically, it is difficult to tell whether small singular values are valid or simply machine noise in computing a $0$ singular value. This requires a threshhold to determine which singular values are discarded.

Let's look at the SVD in detail.

Singular Value Decomposition

Every matrix $$ \mathbf{A} \in \mathbb{C}^{m\times n}_{\rho} $$ has a singular value decomposition of the form $$ \begin{align} \mathbf{A} &= \mathbf{U} \, \Sigma \, \mathbf{V}^{*} \\ % &= % U \left[ \begin{array}{cc} \color{blue}{\mathbf{U}_{\mathcal{R}}} & \color{red}{\mathbf{U}_{\mathcal{N}}} \end{array} \right] % Sigma \left[ \begin{array}{cccc|cc} \sigma_{1} & 0 & \dots & & & \dots & 0 \\ 0 & \sigma_{2} \\ \vdots && \ddots \\ & & & \sigma_{\rho} \\\hline & & & & 0 & \\ \vdots &&&&&\ddots \\ 0 & & & & & & 0 \\ \end{array} \right] % V \left[ \begin{array}{c} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} \\ \color{red}{\mathbf{V}_{\mathcal{N}}}^{*} \end{array} \right] \\ % & = % U \left[ \begin{array}{cccccccc} \color{blue}{u_{1}} & \dots & \color{blue}{u_{\rho}} & \color{red}{u_{\rho+1}} & \dots & \color{red}{u_{n}} \end{array} \right] % Sigma \left[ \begin{array}{cc} \mathbf{S}_{\rho\times \rho} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array} \right] % V \left[ \begin{array}{c} \color{blue}{v_{1}^{*}} \\ \vdots \\ \color{blue}{v_{\rho}^{*}} \\ \color{red}{v_{\rho+1}^{*}} \\ \vdots \\ \color{red}{v_{n}^{*}} \end{array} \right] % \end{align} $$

The connection to the row and column spaces follows: $$ \begin{align} % R A \color{blue}{\mathcal{R} \left( \mathbf{A} \right)} &= \text{span} \left\{ \color{blue}{u_{1}}, \dots , \color{blue}{u_{\rho}} \right\} \\ % R A* \color{blue}{\mathcal{R} \left( \mathbf{A}^{*} \right)} &= \text{span} \left\{ \color{blue}{v_{1}}, \dots , \color{blue}{v_{\rho}} \right\} \\ % N A* \color{red}{\mathcal{N} \left( \mathbf{A}^{*} \right)} &= \text{span} \left\{ \color{red}{u_{\rho+1}}, \dots , \color{red}{u_{m}} \right\} \\ % N A \color{red}{\mathcal{N} \left( \mathbf{A} \right)} &= \text{span} \left\{ \color{red}{v_{\rho+1}}, \dots , \color{red}{v_{n}} \right\} \\ % \end{align} $$ You are using is $\mathbf{S} \, \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*}$. This ignores the null space contributions in red.

---

A rank $\rho = 3$ approximation would look like this; $$ \mathbf{S}_{3} \, \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} = \left[ \begin{array}{cccc|cc} \sigma_{1} & 0 & 0 \\ 0 & \sigma_{2} & 0 \\ 0 & 0 & \sigma_{3} \\ \end{array} \right] % % V \left[ \begin{array}{c} \color{blue}{v_{1}^{*}} \\ \color{blue}{v_{2}^{*}} \\ \color{blue}{v_{3}^{*}} \\ \end{array} \right] % \in \mathbb{C}^{\rho \times n} $$

---

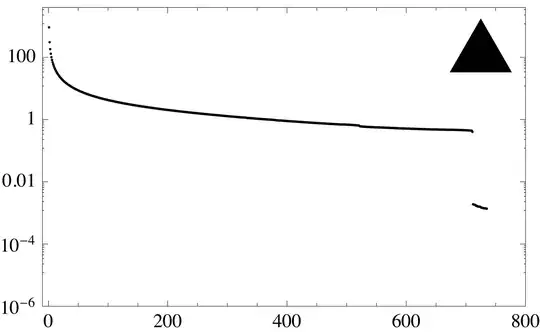
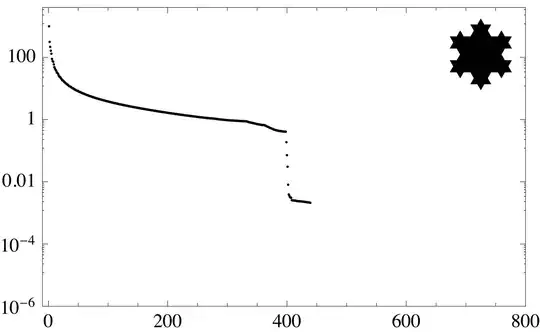
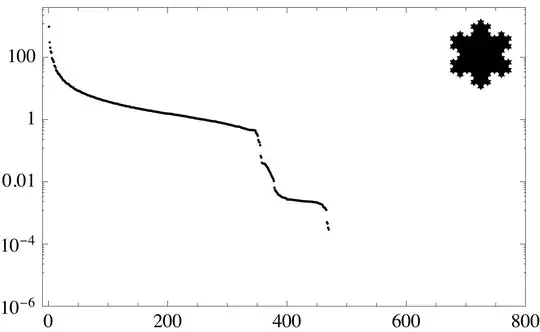
The following sequence shows the Koch snowflake fractals and their singular value spectra. As the object becomes more detailed, the spectrum becomes richer.