2

I have a function $\frac{x^2+2}{x-1}$. I want to find a tangent at a given point of $x=1+\sqrt{3}$. At first, I found a value of the function at given point. This is what I got: $2+\frac{6}{\sqrt{3}}$ Then, I found a derivative of this point and I think it's $0$. So, for me the tangent is $y=(2+\frac{6}{\sqrt{3}})$ but, the proper result is $-2\sqrt{3}-2$. What am I doing wrong?

gymbvghjkgkjkhgfkl
  • 8,090
Radosław Piotrowski
  • 21
  • Your work seems correct, I've tried solving the problem and representing it graphically too. Are you sure you've typed the functions correctly? Out of curiosity, where did you get this 'proper result' from? – projectilemotion Mar 02 '17 at 13:35
  • I removed my 'please show your work' comment, because the calculation is now below... One should of course show one's work, but honestly I was concerned because of your phrase "found a derivative of this point," as opposed to "found the derivative at this point." Best... – peter a g Mar 02 '17 at 13:43
  • 1
    Thanks, I got this "proper" answer from the answer key. It must be wrong. – Radosław Piotrowski Mar 02 '17 at 14:21

4 Answers4

1

Note that $\frac{6}{\sqrt3} = \frac{(2)(3)}{\sqrt3} = 2\sqrt3$

So your $2 + \frac{6}{\sqrt3} = 2\sqrt3 + 2$

So you agree with the answer key with the exception of a sign.

Calculating mentally I agree with your derivative of zero (but yes you should show your work -- easy enough to slip up, especially when I do a mental check.)

So you have to track a sign error. Did you mis-copy, for example was it 1 - x rather than x - 1? Or was there a negative sign in front of the whole fraction? Or did you work this out from a previous problem and maybe lose a sign there?

If, after you have triple-checked everything, a sign error remains, it is possible (rare but possible) that your answer key is in error.

victoria
  • 1,399
  • 6
  • 12
0

$$f(x)=\frac{x^2+2}{x-1}\to f'(x)=\frac{x^2-2x-2}{(x-1)^2}=1-\frac{3}{(x-1)^2}\to f'(1+\sqrt{3})=0$$

So the tangent line is given by

$$y=f(1+\sqrt{3})=\frac{(1+\sqrt{3})^2+2}{\sqrt{3}}=2+\frac{6}{\sqrt{3}}=2+2\sqrt{3}$$

Arnaldo
  • 21,342
0

Your work seems correct.

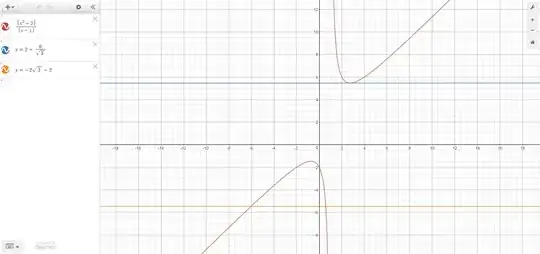enter image description The $\color{red}{\text{red}}$ line is your function and the $\color{blue}{\text{blue}}$ line is the tangent line you've derived. The $\color{orange}{\text{orange}}$ line is the tangent line given by your answer key.

Also, note that your tangent line can be simplified to: $$y=2+\frac{6}{\sqrt{3}}=2+\frac{2\cdot 3}{\sqrt{3}}=2+2\sqrt{3}$$

projectilemotion
  • 15,428
0

The derivative of a function $f$ at a point $x_0$ is the slope of the tangent line to $f$ at $x_0.$

So, let $f(x)=\frac{x^2+2}{x-1}$ and $x_0=1+\sqrt{3}.$ $$\Rightarrow f'(x)=\frac{(x-1)\cdot 2x - (x^2+2)\cdot 1}{(x-1)^2}=\frac{x^2-2x-2}{(x-1)^2}.$$ and $$f'(x_0)=f'(1+\sqrt{3})=\frac{(1+\sqrt{3})^2-2(1+\sqrt{3})-2}{(1+\sqrt{3}-1)^2}=0.$$ Now, to get the equation of the line we have $$y-f(x_0)=f'(x_0)(x-x_0)$$ but $f'(x_0)=0$ so we have $$y=f(x_0).$$ $$\Rightarrow y=f(x_0)=f(1+\sqrt{3})=\frac{(1+\sqrt{3})^2+2}{(1+\sqrt{3})-1}=\frac{6+2\sqrt{3}}{\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}=\frac{6\sqrt{3}+6}{3}=2\sqrt{3}+2.$$ Therefore, $$y=2\sqrt{3}+2.$$

desperatemuch
  • 168