Intuition and the fundamental theorem of calculus

Question

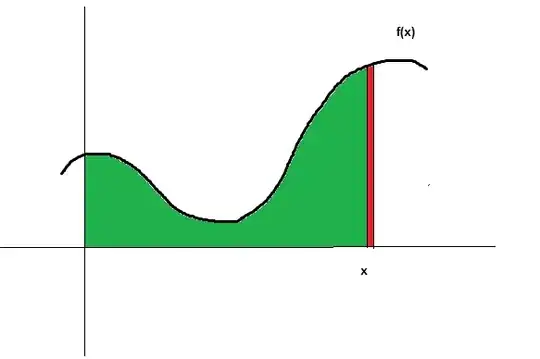
I think the following example explains the fundamental theorem of calculus quite intuitively. Or more precisely, that's what I thought; now I'm starting to have some doubts.

Suppose $v(t)$ is the velocity of a car driving along the highway. The units for $t$ are in hours and the units for $v(t)$ are in miles per hour. Assume $v(t)$ is continuous and nonnegative. What is the displacement of the car over one hour (ie., $t \in [0,1]$)?

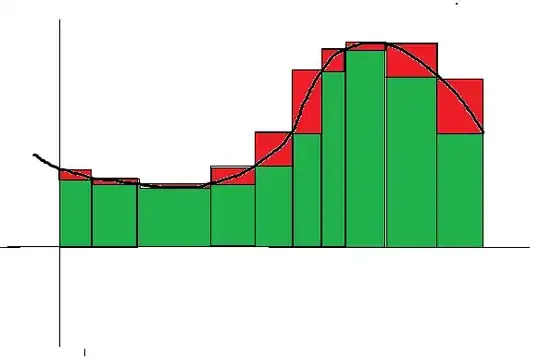
Well, if we subdivide $[0,1]$ into $n$ subintervals of equal length, in each subinterval $\left[\frac{k}{n}, \frac{k+1}{n}\right]$ the velocity doesn't change too much for large $n$ and hence can be approximated by $v(\frac{k}{n})$. Therefore, the displacement in $\left[\frac{k}{n}, \frac{k+1}{n}\right]$ is equal to $\frac{1}{n} v(\frac{k}{n}) + \epsilon(k, n)$ where $\epsilon(k, n)$ is a small error dependent on $k$ and $n$.

Hence $$ \text{Displacement} = x(1) - x(0) = \sum_{k=0}^{n-1} \frac{1}{n} v\left(\frac{k}{n}\right) + \sum_{k=0}^{n-1} \epsilon(k, n) $$

Note that the above equality holds for all $n$, since we have accounted for the error. If we assume that $ \sum_{k=0}^{n-1} \epsilon(k, n) \to 0$ as $n \to \infty$, then it's easy to see that $$x(1) - x(0) = \lim \sum_{k=0}^{n-1} \frac{1}{n} v\left(\frac{k}{n}\right) = \int_0^1 v(t) \ dt$$

However, it's not obviously clear to me why $\sum_{k=0}^{n-1} \epsilon(k, n) \to 0$ as $n \to \infty$. Why should this hold intuitively?

Answer 1

The function $v$ is uniformly continuous on $[0,1]$. Given any $\epsilon > 0$, there is an $N$ such that whenever $n \geq N$, we have, for all $k$ and all $x \in [k/n, (k+1)/n]$, the inequality $|v(x) - v(k/n)| \leq \epsilon$. Thus your error $\epsilon(k,n)$ is bounded in absolute value by $\epsilon/n$. Summing over $k$, the total error in the displacement is bounded in absolute value by $\epsilon$, so long as $n \geq N$.

Answer 2

In broad strokes:

Suppose $F(x)$ is the cumulative area under the curve of $f(x)$ from $0$ to $x$ i.e. the green region below?

What is the derivative of $F(x)$? How fast is $F(x)$ changing as $x$ changes?

$F(x+h)-F(x)$ is the red region.

$F'(x) = f(x)$

Update:

The Riemann Sum.

We can partition the domain

$a=x_0<x_1<x_2<\cdots<x_i<\cdots<x_n =b$

$\int_a^b f(x) dx = \sum_{i=1}^{n} f(x_i^*)(x_i - x_{i-1})$

Where $x_i^*\in [x_{i-1},x_i]$

I say, that if the partition is fine enough, it does matter if we take the biggest possible value of $f(x_i^*)$ the smallest or something in between.

Suppose we choose $x_i^*$ to always produce the smallest $f(x_i)$. We would call this the lower sum, and we would get the green area.

And if we choose $x_i^*$ to produce the largest $f(x_i)$ we get the upper sum. The green + red.

And the difference is just the red boxes.

As the partition gets to be increasingly fine, the errors (the red boxes) only get smaller, and eventually their net area goes to 0.