5

Let $a,b,c,d$ and $,e$ are non-negatives .show that

$$(a+b+c+d+e)^3\geq9(2abc+abd+abe+acd+ade+2bcd+bce+bde+2cde),$$

Michael Rozenberg says that this inequality proof is very ugly.

I think this inequality seems nice and maybe it has simple methods to solve it?

Community
  • 1
math110
  • 93,304
  • 1
    Most inequalities I've seen here are not so nice and do not not have simple methods to solve. – Han de Bruijn Mar 30 '17 at 18:01
  • For conext, the source of this question is http://math.stackexchange.com/q/2201085 (as I found in the edit history). It's too late now, but I would have suggested that you put you bounty directly over there, which I presume is the question you actually care about. It's much nicer than this, which does not seem nice at all – echinodermata Apr 01 '17 at 18:32
  • Maybe you could compute all partial derivatives to show that after some value $a+b+c+d+e=x$, $(a+b+c+d+e)^{3}$ is growing faster than messy RHS, then just check the finite cases directly, hopefully there are not many. – Mars Apr 05 '17 at 09:33
  • @echinodermata There are two different questions.Issue question has a nice form and routine way to solution, and this vice versa. – Yuri Negometyanov Apr 10 '17 at 12:08
  • 1
    @Morph It is much easier to apply the method of Lagrange multipliers to the original equation. But it's not so interesting. – Yuri Negometyanov Apr 10 '17 at 12:13

1 Answers1

6

At first, from AM-GM: $$\frac13(a+b+c+d+e)^3 \ge 9(a+b)c(d+e) = 9(acd+bcd+ace+bce),$$ and similarly for any permutations of $a,b,c,d,e.$ So it requres to find only 3 of them, the sum of which gives RHS of original inequality.

Taking in account that RHS of original inequality doesn'n contain the term $ace,$ one can obtain only 9 variants of satisfying permutations. One of its combinations can lead to goal.

Easy to see that there are only 6 pairs of permutations which gives the term $2abc$ in sum. Third permutation can be found among another permutations.

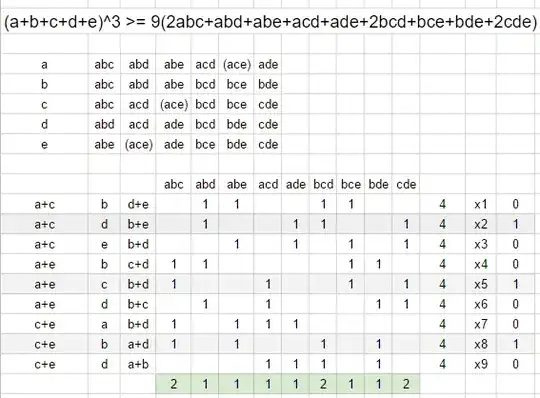
Checking of them with Google Sheets gives required triple. picture

Finally, $$(a+b+c+d+e)^3 \ge 9((a+c)d(b+e) + (a+e)c(b+d) + (c+e)b(a+d)),$$ $$\boxed{(a+b+c+d+e)^3\geq9(2abc+abd+abe+acd+ade+2bcd+bce+bde+2cde).}$$

Yuri Negometyanov
  • 28,026