Average Rate of Change of Functions

Question

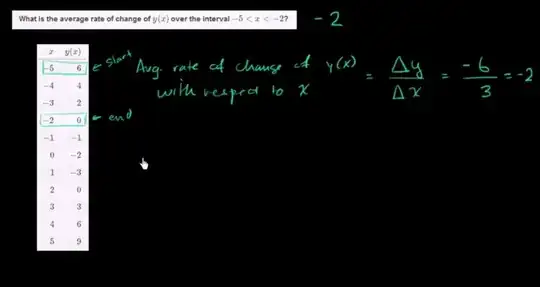
In here to find out the average rate of change -5 and 2 were used. But I'm wondering why, because in the interval these aren't included. Wouldn't it only be correct using -5 and -2 to solve the problem if the interval was -5<=x<=-2?

Answer 1

Let us assume that the real-valued function $y(x)$ is continuous on $[-5,-2]$ and differentiable on $(-5,-2)$. If so, we can apply the Mean Value Theorem (MVT or LMVT) and find the average rate of change of $y(x)$ over the interval $-5\le x\le-2$ as equal to the slope of the tangent line at some point $c\in(-5,-2)$ that is guaranteed to exist. $$y'(c)=\frac{\Delta y}{\Delta x}=\frac{y(-2)-y(-5)}{-2-(-5)}=\frac{0-6}{-2+5}=\frac{-6}{3}=-2$$ In regards to your comment, the inequality symbols $\lt$ and $\le$ are not the same. You are right to be mindful of the applicability of certain statements and theorems on certain intervals, but we are permitted to apply the MVT here in this problem. Also, because we assumed that $y(x)$ is continuous at $x=-2$, we assumed the quintessential requirement for continuity at $x=-2$. $$\lim\limits_{x\to-2}(y(x))=y(-2)=0$$ The left-side and right-side limits must be equal for the ordinary limit to exist, and $x\to-2^-$ implies $x\lt-2$. The same reasoning can be said for $x=-5$, particularly $x\to-5^+$ meaning $x\gt-5$. Thus, if you want to be particularly meticulous, the average rate of change of $y(x)$ on $(-5,-2)$, the interval in the problem, approaches the same amount as on $[-5,-2]$ as we established, all things considered.