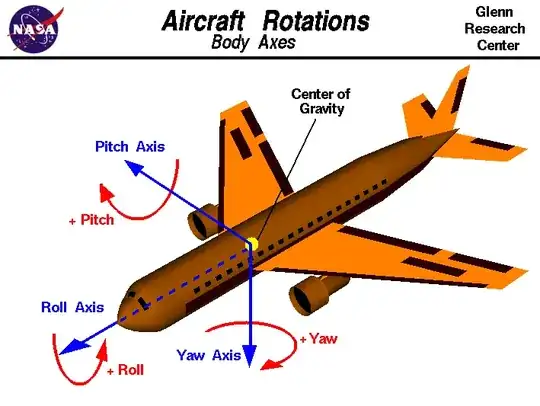
I need to transform any arbitrary vector in a fixed cartesian coordinate system (let's call this coordinate system $(1)$) to a different cartesian coordinate system (let's call it $(2)$). For illustration, $(1)$ is attached to this airplane where the roll axis is x, the pitch axis is y, and the yaw axis is z:
$2$ is defined a coincident origin to (1) with x2 pointing North, y2 pointing East, and z2 pointing along the resultant nadir radial line. I need to be able to take any vector in (1) and find its coordinates in (2) given the yaw, pitch, and roll of the aircraft.
From the linear algebra that I know, any point in (1) (let's call it $P_{1}$) should be able to be transformed from (1) to (2) by use of a 3x3 Matrix $A$. Thus, the resultant point $P_{2}$ can be found using
$$P_{2}=AP_{1}$$
My problem is finding what A is. While A can be decomposed into separate transformations by rotating about the x1 y1 and z1 axes of (1) separately using separate rotation matrices, my work up to this point has lead me to conclude that those separate rotations cannot be easily phrased in terms of the yaw pitch and roll angles that I have. Specifically, it seems that three separate transformations about the x y and z axes of (1), using transformation matrices X, Y, and Z respectively, are extrinsic transformations (all the transformations move the vector being transformed relative to (1) throughout the transformation process). Mathematically, these extrinsic rotations are performed by $$P_{2}=XYZP_{1}$$ I am aware that the order of X,Y, and Z is important since $AB\neq BA$. I also am not sure what order they should be in.
Ideally, what I would like is to mathematically transform the vector through intrinsic rotations. Specifically, I would first like to transform $P_{1}$ in (1) by a rotation about $z_{1}$ (a yaw). Then take the new orientation of the plane and define axes $x_{1}'$, $y_{1}'$, and $z_{1}'$ along the new roll pitch and yaw axes of the plane. Then I'd like to be able to perform a pitch transformation about the $y_{1}$' axis to get new axes $x_{1}'', y_{1}'', and z_{1}''$. Then finally, the roll transformation about the $x_{1}''$ axis to get axes $x_{2}, y_{2}, and z_{2}$.
If such intrinsic rotations are not possible to perform separately, then how do I setup A so that I can input the yaw pitch and roll angles, and get $P_{2}$ out?