0

I'm sure this is an easy question for someone, but it's been a while since I've done probability and statistics.

Essentially, after doing some analysis, I have the distribution I'd like to fit for some data

$D = A(\sin(\phi_1) + \sin(\phi_2) + \sin(\phi_3) + \sin(\phi_4)) + B \quad \text{where} \quad \phi_1,\phi_2,\phi_3,\phi_4$ ~ i.i.d.unif$\left(0, \frac{\pi}{2} \right)$

At the moment I'm after the PDF (probability density function) of $D$.

I tried using MGF methods to find the PDF of $D$. Using the fact that $\phi_1,\phi_2,\phi_3,\phi_4$ are iid,

$\begin{align*} M_{D}(t) =E\left[e^{t\sum_{i=1}^{4}\left(A\sin\left(\phi_{i}\right)+B\right)}\right] =E\left[e^{t\sum_{i=1}^{4}\left(A\sin(\phi_{i})+B\right)}\right] =E\left[\prod_{i=1}^{4}e^{\left(A\sin(\phi_{i})+B\right)}\right] \end{align*}$

Now I'm after the MGF of $A\sin(\phi_1) + B$

I had a look at this question: Distribution of sine of uniform random variable on $[0, 2\pi]$. But, the PDF didn't make too much sense to me because I would expect the mode of $A\sin(\phi)$ to be ~$\frac{A}{2}$ whereas the PDF of the Arcsine distribution is highest at its tails? (see edit)

So, I had a go at finding the MGF myself but I hit a brick wall at

$M_{D_1} = E\left[e^{t\left(A\sin\left(\phi_{1}\right)+B\right)}\right] = \ldots = \frac{2}{\pi} \intop_0^\frac{\pi}{2} e^{t(A\sin(\phi) + B)} \,\text{d}x \quad$ ...

My other thought was because $D_1 = A\sin(\phi_1)+B$ is monotonically increasing for $\phi_1 \in \left[0, \frac{\pi}{2}\right]$ I can directly find the PDF as

$f_{D_1} = f_{\phi_1} \left( \arcsin{\left(\frac{D_1 - B}{A}\right)}\right) \times A\cos(\phi_1)\quad$ but that's as far as I've gotten... I haven't got a joint PDF yet

Any help would be much appreciated, thanks!

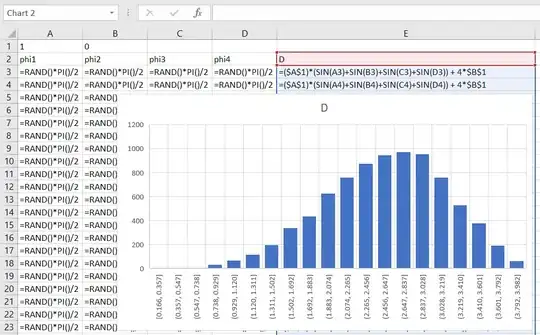
Quick edit for clarity: I did run a numerical simulation with $A=1$ and $B=0$ in Excel as a sanity check that the mode would occur around the middle. For a single $\phi_1$, yes the mode is at the tail but the joint distribution's mode is were I expect it to be. Excel Simulation

Alwin
  • 161
  • 6
  • 1
    "the PDF didn't make too much sense to me because I would expect the mode of Asin(ϕ) to be ~A/2 whereas the PDF of the Arcsine distribution is highest at its tails" If this is the reason why you post the present question, I see no way out... Yes, whether you feel comfortable with the notion or not, the PDF of the standard Arcsine distribution is highest at the boundaries of the interval $(-\pi/2,\pi/2)$, hence in your case, the mode of $A\sin\phi$ is at $A$. – Did May 29 '17 at 09:45
  • @Did thanks for the comment. I was only looking at the join distribution when I should have started with the PDF of a single distribution first, thanks! – Alwin May 29 '17 at 10:09

1 Answers1

1

To avoid (annoying) parameters $A,B$ break it up in the following steps:

  1. find the PDF of $\sin\phi$ where $\phi$ has uniform distribution on $(0,\frac12\pi)$.

  2. find the PDF of $X:=\sum_{i=1}^4\sin\phi_i$ and denote it by $f_X$.

  3. find the PDF of $D:=AX+B$.

The first step results in a function that takes value $\frac2{\pi\sqrt{1-u^2}}$ on $(0,\frac12\pi)$ and takes value $0$ otherwise. Just realize that for $u\in(0,1)$, i.e. in the support of $\sin\phi$, we have: $$\{\sin\phi\leq u\}=\{\phi\in(0,\arcsin u]\}$$ so that the CDF of $\sin\phi$ takes value $\frac2{\pi}\arcsin u$ on $(0,\frac{\pi}2)$. The PDF is found as its derivative.

The second step is in my perception the most difficult one and can be solved with convolutions.

The third step (completely devoted to a return of the parameters) is easy: $f_D(x)=\frac1{|A|}f_X(\frac{x-B}{A})$

drhab
  • 151,093