25

If we allow the standard parabola to rotate, dilate and freely move across a Euclidean plane, then we can define at least one parabola from any 3 distinct points not aligned on a straight line.

Is this parabola unique? If not, how many different parabolas can be formed from any 3 distinct points?

My intuition tells me 3, but I'm not seeing any obvious way to show this (if it's accurate, that is).

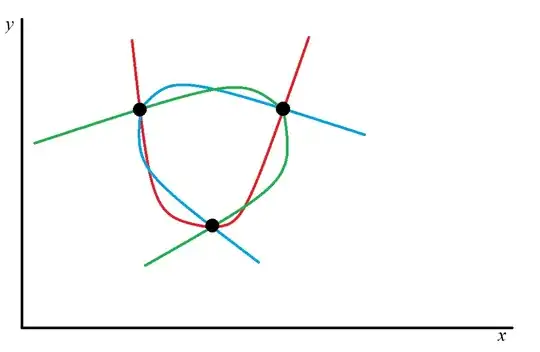
A quick sketch of what I mean (sorry for the poor drawing accuracy) enter image description here

Here we have 3 parabolas being formed by the same 3 distinct points.

Stephen
  • 3,682

4 Answers4

36

There are infinitely many.

Given three non collinear points, you can uniquely define a parabola of the form $y = a(x+b)^2+ c$ which passes through the three points. Now rather than rotating the "parabola", think in terms of rotating the plane.

Define new axes $y'$ and $x'$, so that both of them have been rotated by some $\theta$ from $x$ and $y$. Then your three points are still not collinear, and you can find a parabola $y'=a'(x'+b')^2+c'$ which passes through the points. This parabola is "pointing in the $y'$ direction" (I'm not sure what the terminology is, but I mean a tangent to the vertex of the parabola is parallel to the $x'$ axis.) But then $y$ and $y'$ are in different directions (shifted by $\theta$) so the parabolas must be distinct.

You can do this for all but three values of $\theta$, so there are infinitely many choices of $\theta$, and hence infinitely many parabolas. (Check the comments under my answer to see why three values of $\theta$ don't work.)

Harambe
  • 8,230
  • "still not collinear" may fail - but only in three out of continuum-many cases – Hagen von Eitzen Jun 02 '17 at 06:23
  • 5
    Actually you cannot do it for every $\theta$, as for some values of $\theta$, two of the points will have the same $x'$, and therefore there cannot be a function whose graph goes through both points in that coordinate system. Of course that doesn't really change your argument, as there are only three such exceptions. – celtschk Jun 02 '17 at 06:24
  • 1
    Nice, thank you, I didn't think about that case. – Harambe Jun 02 '17 at 06:25
  • @HagenvonEitzen: Three points are collinear if they lie on a common straight line. Since rotations map straight lines to straight lines, collinearity is preserved by them. I guess you thought of the condition of two points being vertically aligned. – celtschk Jun 02 '17 at 06:26
  • 3
    I wouldn't say "vertex of the parabola is parallel to the $x′$ axis": the vertex is a point and thus isn't parallel to anything. (Perhaps you mean the tangent line to the parabola at the vertex?) But you could also just say that the parabola's axis of symmetry is parallel to the $y'$ axis. – Greg Martin Jun 02 '17 at 07:44
  • But why must the parabolas in the different $x'$, $y'$-planes be oriented as you describe? With the tangent on their vertex parallel to the $x'$-axis? – Stephen Jun 02 '17 at 17:00
  • @celtschk it isn't really a concern if two points have the same $x'$ value as we are not so much study functions rather algebraic varieties – Birch Bryant Jun 03 '17 at 16:25
  • @user253929: Shaneye2020's ansatz is exactly to look at it as rotated functions; therefore it fails for those rotations where there's no such function. This ansatz works for parabolas because there's always a rotation where the rotated parabola is described by a quadratic function. – celtschk Jun 04 '17 at 08:04
25

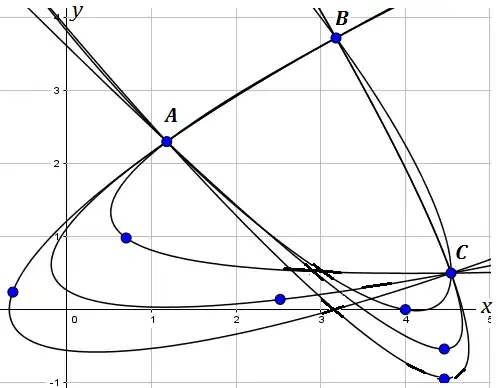
A general conic is defined by five independent parameters and can pass through five arbitrary points.

Restricting to a parabola sets a constraint on the coefficients (the discriminant of the second degree terms must be zero), which "consumes" one degree of freedom.

But four remain, and you have an infinity of parabolas by the three given points and a fourth free one.

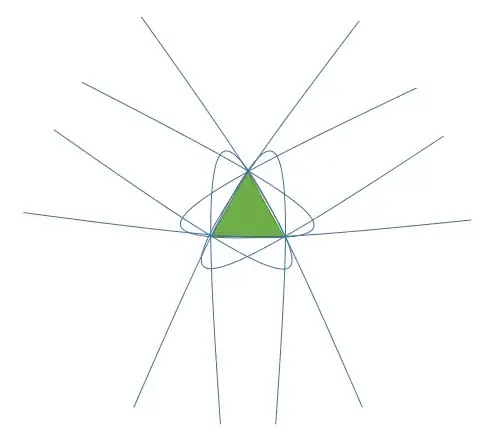
A more difficult question is when the shape of the parabola is fixed, i.e. you can only translate it and rotate it. Then it has only three degrees of freedom and the number of solutions must be finite. In the case of the vertices of an equilateral triangle, there can be at least six of them, by symmetry, as the figure shows.

enter image description here

In the general case, let the parabola have the equation $x=ay^2$, where $a$ is fixed. Then integrating the rigid transform, we need to solve the system

$$\begin{cases} x_0\cos\theta-y_0\sin\theta+t_x=a(x_0\sin\theta+y_0\cos\theta+t_y)^2\\ x_1\cos\theta-y_1\sin\theta+t_x=a(x_1\sin\theta+y_1\cos\theta+t_y)^2\\ x_2\cos\theta-y_2\sin\theta+t_x=a(x_2\sin\theta+y_2\cos\theta+t_y)^2\\ \end{cases}$$

for $\theta, t_x$ and $t_y$.

By subtraction, we can eliminate $t_x$ and we get two equations linear in $t_y$. $$\begin{cases} x_{01}\cos\theta-y_{01}\sin\theta=a(x_{01}\sin\theta+y_{01}\cos\theta)(x'_{01}\sin\theta+y_{01}\cos\theta+2t_y)\\ x_{02}\cos\theta-y_{02}\sin\theta=a(x_{02}\sin\theta+y_{02}\cos\theta)(x'_{02}\sin\theta+y'_{02}\cos\theta+2t_y)\\ \end{cases}$$

Then eliminating $t_y$, we obtain a cubic polynomial equation in $\cos\theta$ and $\sin\theta$. We can rationalize it with the transform

$$\cos\theta=\frac{t^2-1}{t^2+1},\sin\theta=\frac{2t}{t^2+1}.$$

This turns the trigonometric equation in a sextic one, having up to six real solutions.

The detailed discussion of the number of real roots seems to be an endeavor. As the minimum radius of curvature is $2a$, when the circumscribed circle of the triangle is smaller than this value, there is no solution.

  • In the case of the vertices of an equilateral triangle, there are at most six solutions, surely? (There may only be three.) – TonyK Jun 02 '17 at 12:58
  • @TonyK: you are right. What I meant is that the figure proves a case with at least six solutions, which is the general situation (I didn't want to comment about the possible degeneracy). By the way, the rest of my answer proves at most six, so that the figure is actually exhaustive. And as I said, discussing the exact number of solutions may be arduous. –  Jun 02 '17 at 13:21
  • Yes. I recommend changing "at least" (which is simply wrong) to "in general". – TonyK Jun 02 '17 at 13:31
  • @TonyK: I want to express that the figure only proves a lower bound, other solutions might exist. –  Jun 02 '17 at 13:36
  • But it doesn't prove a lower bound! The lower bound is three. – TonyK Jun 02 '17 at 13:37
  • 1
    @TonyK: you didn't listen. On that figure there are at least six solutions. And by the way, the general lower bound for an equilateral triangle is zero. –  Jun 02 '17 at 13:38
6

Three points determine a circle anyway you wish to place them

Four points determine two unique parabolas (as mentioned by ccorn) anyway you wish to place them, subject to convexity and other conditions to avoid degeneracy also as stated by him.There is a doubly infinite set, a new rough sketch indicates both.

Five points determine a conic anyway you wish to place them.

There are infinitely many parabolas through 3 given points.

It can be seen that a parabola equation (eccentricity $ \,e\,= 0$) can be expressed from standard conics definition as

$$ y = C_1x+ C_2 \pm \sqrt {C_3x+ C_4} \tag1 $$

Out of four arbitrary constants if three points are given, then you have a singly infinite set of parabolas through them as shown, 3 points $(A,B,C) $ are fixed and a fourth coincident/double point carefully chosen from Geogebra to form a parabola.

So from the above if you choose one rigid parabolic arc among them, then there is a unique way to fit it back after removing from the 3 given points to re-assemble it.

When fourth point is Java dragged/moved a bit to right along the normal it forms an ellipse and when moved left, a hyperbola. Along the parabola any motion leaves it unchanged proving that the drawn curve is indeed a parabola..standing in its rightful place between the ellipse and the hyperbola. Shown here are three for each set but there are infinitely many for each.

Doubly infinite set of Parabolas

Narasimham
  • 40,495
  • "a parabola anyway you wish to place them": aren't there impossible configurations such as the four vertices of a square ? –  Jun 02 '17 at 08:47
  • 1
    It is singular case but not impossible case .For the 4 points vertexed at $(\pm1,\pm1)$ the parabola can reduce to either one of two pairs of straight lines $(x^2-1)=0, (y^2-1)=0$ – Narasimham Jun 02 '17 at 09:34
  • Can one decently call that a parabola ? –  Jun 02 '17 at 09:42
  • 1
    Yes, degenerate case. A pair of straight lines.If an isosceles trapezium made into a square/rectangle, it has nowhere to go. – Narasimham Jun 02 '17 at 10:04
  • 1
    Re: Four points determine a parabola anyway you wish to place them. No: The four points need to form a strictly convex polygon, and then there are two parabolas that pass through those four points. Newton has presented a solution to the problem of constructing (with straightedge and compass) the foci and directrices of those two parabolas, when given the four points. – ccorn Jun 02 '17 at 10:33
  • To be more precise, the conditions on the four points are: Pairwise distinct; no parallel secants (to rule out the degenerate cases, this also implies that no three points are collinear); and no point is allowed to lie in the triangle formed by the other three. That there can be two fitting parabolas can be seen intuitively by reversing the process: Intersect two different parabolas, that gives up to four points, and such four points form a configuration with the properties described above. That there are exactly two such parabolas can be shown algebraically. – ccorn Jun 02 '17 at 11:01
  • Java moved....? – user253751 Jun 02 '17 at 12:01
  • I mean dragging/moving the point of a curve by click/holding with mouse pointing. – Narasimham Jun 02 '17 at 12:21
  • @ccorn: I did suspect that such a limitation existed. Thanks for this contribution. –  Jun 02 '17 at 12:28
  • By the way, parabolas have eccentricity $1$, not $0$. :-) – ccorn Jun 02 '17 at 13:14
  • Why can we not duplicate Newton's construction with Geogebra or other graphing aid? Can you please give Newton's Ruler/Compass reference? – Narasimham Jun 02 '17 at 13:26
  • 1
    The Newton reference is mentioned by H. Dörrie (1965): 100 Great Problems of Elementary Mathematics. Page 208, problem 45: A Parabola from Four Points. Translation by D. Antin from Dörrie's german 1958 original Triumph der Mathematik: Hundert berühmte Probleme aus zwei Jahrtausenden mathematischer Kultur. The construction is also given in H. T. Eagles (1885): Constructive Geometry of Plane Curves. Macmillan & Co. London, Cambridge University Press. Page 87, Problem 56 (Fig. 52): To draw a parabola to pass through four given points A,B,C,D. – ccorn Jun 02 '17 at 14:03
  • Construction hints: Look at that figure. This does a graphical geometric-mean construction that yields the two possible directions for the parabola's axis of symmetry (dash-dotted lines $d_1,d_2$). The rest is quite straightforward: – ccorn Jun 02 '17 at 14:45
  • Construct the three $Q$ points mentioned in item (1) of that answer. Their pairwise midpoints form a triangle $\Delta$. Now each parabola has $\Delta$'s produced sides as tangents; its directrix (which is orthogonal to the axis of symmetry) passes through $\Delta$'s orthocenter; and its focus can be obtained as the intersection of the mirror images of the directrix across $\Delta$'s sides. By Lambert's theorem, the focus will end up on the circumcircle of $\Delta$. – ccorn Jun 02 '17 at 14:45
  • Thanks. It is possible to approximately construct both the unique parabolas using e.g., Geogebra adjusting coincident points.Shall modify the sketch.Also the analytic solution is quite cumbersome. – Narasimham Jun 03 '17 at 12:54
3

A parabola is a conic with a double point at infinity. For each point on the line at infinity other than the three points corresponding to the three lines determined by the given three points, there is a unique parabola through the given three points not on a line. so there are a continuum of them.

R.C.Cowsik
  • 343