0

My question is about Huffman codes. Consider a random variable $X$ which takes $6$ values $A, B, C, D, E, F$ with probabilities $(0.5, 0.25, 0.1, 0.05, 0.05, 0.05)$ respectively. We want to construct a binary Huffman code for it. Here in the solution it has constructed these codes:

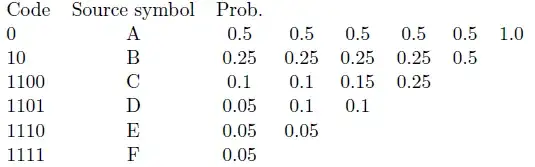
enter image description here

But I solved it myself and find different codes:

enter image description here

My codes are these: $(A=0, B=10, C=111, D=1101, E=11000, F=11001)$

Although average length of both codes are the same and is equal to 2, the codes are different(for example in the first one, the length of C is 4, but in the second one, its length is 3). I wanted to know why this difference happens and which one is correct and standard?

Community
  • 1
helen
  • 249

1 Answers1

1

Such difference can well occur whenever there are some "ties" in the ordered probabilities. No problem. Both are correct Huffman codes.

There is no standard "tie-breaker" rule. And usually that doesn't matter. What matters is consistency: if the decoder must reconstruct the encoding tree, then both the encoder and then decoder must stick to some common (arbitrary but predetermined and deterministic) tie-breaker rule.

Another consideration is that the alternative codes, in spite of having the same average code length, will in general have different variance. Because one usually prefers smaller variances, one might want to use that as a criterion (see eg here , section 3). That, still might be insufficient to break all ties.

leonbloy
  • 63,430
  • So according to what you said, my solution and the codes which i created doesn't have any problem and can be used as Huffman codes. Right? – helen Jun 09 '17 at 06:29
  • Yes. Your code (in singular; there are six codewords, but the code is one) is a well constructed Huffman code. – leonbloy Jun 09 '17 at 11:03