I am experiencing difficulties computing the integral
$$\int_0^{+\infty}\int_0^t \frac{s^{c}t}{(s^2+a)^b(t^2+a)^b} \,ds\,dt.$$,
where $a$, $b$ and $c$ are positive numbers.
I would be thankful if someone could suggest an approach to its solution.
Thanks everyone in advance!
HINT : $$\text{Let}\qquad I(M)=\int_0^{M}\int_0^t \frac{s^{c}t}{(s^2+a)^b(t^2+a)^b} \,ds\,dt \qquad\text{with}\quad M>0\tag 1$$ One little picture says more than a long speech!
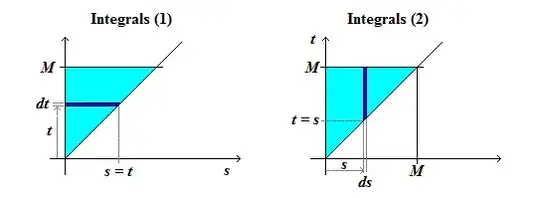
$$I(M)=\int_0^{M}\int_s^{M} \frac{s^{c}t}{(s^2+a)^b(t^2+a)^b} \,dt\,ds.\tag 2$$ $$I(M)=\int_0^{M}\frac{s^{c}}{(s^2+a)^b}\left(\int_s^{M} \frac{t}{(t^2+a)^b} \,dt\right)\,ds.$$ $\int_s^{M} \frac{t}{(t^2+a)^b} \,dt= \frac{1}{2(b-1)(s^2+a)^{b-1}}-\frac{1}{2(b-1)(M^2+a)^{b-1}} $
$$I(M)=\frac{1}{2(b-1)}\int_0^{M}\frac{s^{c}}{(s^2+a)^{2b-1}} \,ds - \frac{1}{2(b-1)(M^2+a)^{b-1}}\int_0^{M}\frac{s^{c}}{(s^2+a)^{b}}\,ds $$ For $M\to\infty$ the second term which is equivalent to $\frac{1}{2(b-1)(c-2b+1)M^{c-4b+3}}$ tends to $0$ if $b>1+\frac{c}{4}$.
The condition of convergence of the first integral is $b>1+\frac{c}{4}$. $$\int_0^{+\infty}\int_0^t \frac{s^{c}t}{(s^2+a)^b(t^2+a)^b} \,ds\,dt =\frac{1}{2(b-1)}\int_0^{+\infty}\frac{s^{c}}{(s^2+a)^{2b-1}} \,ds $$ I suppose that you can take it from here.
