According to Wolfram Alpha, "Abel's Integral" is the following, and it's value is found in the method indicated below. I am unable to see how line 6 is obtained. $$$$ 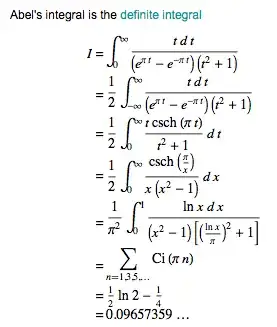
- 1,082
2 Answers
Note that $$\frac{b}{{{b^2} + 1}} = \int_0^\infty {{e^{ - bx}}\cos xdx} $$ Hence $$\int_0^\infty {\frac{x}{{{x^2} + 1}}{e^{ - ax}}dx} = \int_0^\infty {\int_0^\infty {{e^{ - xt}}(\cos t){e^{ - ax}}dt} dx} = \int_0^\infty {\frac{{\cos t}}{{t + a}}dt}$$ this gives $$\text{Ci}(\pi n) = {( - 1)^{n + 1}}\int_0^\infty {\frac{x}{{{x^2} + 1}}{e^{ - \pi nx}}dx}$$ Summing over $n=1,3,5...$ gives $$\sum_{n = 1,3,5...}\text{Ci}(\pi n) = \int_{0}^{\infty} \frac{x}{(x^2+1)(e^{\pi x}-e^{-\pi x})} dx$$
This is line 6.
For the evaluation of the integral, consider
$$ \mathcal{I} = \int_{-\infty}^{\infty} \frac{x}{\sinh(\pi x)(1+x^2)}dx $$
Consider the rectangular contour with vertices $R, R+Ri, -R+Ri, -R$, where $R=2N+1/2$ with $N$ a very large integer. When $R$ tends to infinity, the following three integrals tend to 0 $$\int_{R}^{R+Ri} \frac{x}{\sinh(\pi x)(1+x^2)}dx \to 0$$ $$\int_{R+Ri}^{-R+Ri} \frac{x}{\sinh(\pi x)(1+x^2)}dx \to 0$$ $$\int_{-R+Ri}^{-R} \frac{x}{\sinh(\pi x)(1+x^2)}dx \to 0$$
Note that the function $\dfrac{z}{\sinh(\pi z)(1+z^2)}$ has simple pole at $z=ni$, with $n\geq 2$ and a double pole at $z=i$, the residue at $z=ni$ being $\dfrac{(-1)^n(ni)}{\pi(1-n^2)}$, and at $z=i$ being $\frac{i}{4\pi}$.
Hence $$\begin{aligned} \mathcal{I} &= 2\pi i\frac{i}{4\pi} + 2\pi i\sum_{n = 2}^{\infty}\frac{(-1)^n(ni)}{\pi(1-n^2)} \\ &= -\frac{1}{2}+2\sum_{n = 2}^{\infty}\frac{(-1)^nn}{n^2-1} \\ &= -\frac{1}{2}+\sum_{n = 2}^{\infty}\left(\frac{(-1)^n}{n-1}+\frac{(-1)^n}{n+1}\right) \\ &= 2\ln 2 -1 \end{aligned} $$
- 18,983
-
I apologize if this is a frustrating request, but would you mind demonstrating how one would actually go about evaluating the integral? – BelowAverageIntelligence Jun 17 '17 at 00:27
-
-
When you say "a double pole at n=i" do you mean at z=i? – BelowAverageIntelligence Jun 17 '17 at 07:53
-
-
-
I ask because R, R+Ri, and R-Ri all lie on the line where Re (z)=R. – BelowAverageIntelligence Jun 19 '17 at 12:05
-
-
I'm having trouble getting the residue at z=i. Would you mind explaining how you calculate that? – BelowAverageIntelligence Jun 20 '17 at 11:25
-
Also, can you explain why the three integrals tend to zero and what the significance of that is? – BelowAverageIntelligence Jun 20 '17 at 11:28
-
And is it okay that we have a pole on the boundary of the contour at z=0? – BelowAverageIntelligence Jun 20 '17 at 11:29
-
Three last questions 1) Why do we only care about the part of complex plane where Im(z)>0? 2) What is the significance of R being equal to 2N+1/2? and 3) Why does integrating our function over this rectangular area which spans half of the complex plane give us the integral (which doesn't seem to have that much to do with complex numbers) over the real numbers that we were aiming for? (please correct me if any of the statements I've made here are incorrect). – BelowAverageIntelligence Jun 20 '17 at 11:49
You can use Parseval's theorem $$ \int_{-\infty}^{\infty}f(x)\bar{g}(x)dx=\int_{-\infty}^{\infty}\hat{f}(s)\hat{\bar{g}}(s)ds $$ to evaluate this integral. Let $$ f(x)=\frac{x}{\sinh(\pi x)}, g(x)=\frac{1}{1+x^2}. $$ Clearly $$ \hat{g}(s)=\sqrt{\frac{\pi}{2}}e^{-|s|}. $$ From this, one has $$ \hat{f}(s)=\frac{1}{2\sqrt{2\pi}\cosh^2(\frac{s}{2})}. $$ So \begin{eqnarray} \int_{0}^{\infty}f(x)g(x)dx&=&\frac{1}{2}\int_{-\infty}^{\infty}f(x)\bar{g}(x)dx\\ &=&\frac{1}{2}\int_{-\infty}^{\infty}\hat{f}(s)\hat{\bar{g}}(s)ds\\ &=&\frac{1}{2}\int_{-\infty}^{\infty}\frac{1}{2\sqrt{2\pi}\cosh^2(\frac{s}{2})}\sqrt{\frac{\pi}{2}}e^{-|s|}ds\\ &=&\frac12(2\ln2-1). \end{eqnarray}
- 44,000
$$ I=\sum_{n\geq0}(-1)^n f(n)-\frac{1}{2}f(0)=-\frac{1}{2}\sum_{n\geq0}\frac{(-1)^n}n-\frac{1}{4}=\frac{1}{2} \log(2)-\frac{1}{4} $$
– tired Jun 16 '17 at 18:09