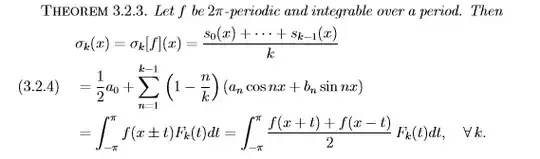0

I'm having trouble proving the following conjecture in $(1.)$, via Fourier methods, my intial attack can be seen in $(2)$

$(1.)$

$$\sin(x) + \sin(2x) + \sin(3x)+ \cdots +\sin(nx) = \frac{cos(1/2) - cos(n-1/2)}{2 \sin(1/2)2}$$  

$(2)$

On the RHS, side of our conjecture of $(1.)$, the following observations can be made due to applying the technique of Ceasro Summation, one can derive the Cesaro means from the RHS of $(2.1)$.

$$[S_{k} = \sin(x) + \sin(2x) + \sin(3x)+ \cdots + \sin (nx) = \sum_{n} \sin(n(x))\tag{2.1}]$$

$$[\sigma_{n} = \frac{\sin(x)) + \sin(2(x)) + \sin(3(x)) + \cdot \cdot \cdot + sin(n(x))_{n-1}}{N} \tag{2.2}]$$

$$[ \sin(x) + (1 - 1/k) \sin(2x) + \cdot \cdot \cdot + (1 - n/k) \sin(n(x)) + \cdot \cdot \cdot \frac{1}{k}\sin(n(x))_{k-1} \tag{2.3}]$$

One, can formally verify the observations made in $(2.2)-(2.3)$, by taking the $\lim_{n \rightarrow \infty}\sigma_{N}$, as follows in $(2.4)$

$$\lim_{n \rightarrow\infty} (\sin(x) + (1 - 1/k) \sin(2x) + \cdot \cdot \cdot + (1 - n/k) \sin(n(x)) + \cdot \cdot \cdot \frac{1}{k}\sin(n(x))_{k-1}) = S$$

Lemma:

Theorem 3.23

The specifics of my questions, lie on applying Theorem $(3.23)$ to the RHS side, of $(2.3)$ for the application of the theorem to be successful it would following from the RHS of $(1.)$ to be written as Fourier polynomials as follows:

$$F_{n}(x) = a_{o}+(a_{1}\cos(x) +b_{1}\sin(x))) + \cdot \cdot \cdot + (a_{n} \cos(n(x) + b_{n}\sin(n(x))$$

Is my approach on the right track any hints would be helpful.

Thomas Andrews
  • 177,126
Zophikel
  • 1,061
  • Considering that the right side doesn't have $x$, you might reconsider. – marty cohen Jun 18 '17 at 15:41
  • Yes that what i'm initially thinking, I was thinking about just representing the RHS and LHS side as Fourier Series and just directly calculate the Fourier Coefficients to show that their equal – Zophikel Jun 18 '17 at 15:42
  • 1
    Cesaro summation is an overkill, you are just dealing with telescopic sums in disguise: https://math.stackexchange.com/questions/17966/how-can-we-sum-up-sin-and-cos-series-when-the-angles-are-in-arithmetic-pro – Jack D'Aurizio Jun 18 '17 at 15:43
  • Looking back it my initial approach was overkill, I wanted to prove this via Fourier Methods looks like I overlooked a lot of things when dealing with this problem. How does avoid going "Overkill" on a problem. Also the book wanted the reader to use a "Fourier Appoarch" when dealing with the problem. – Zophikel Jun 18 '17 at 15:49
  • But was my "Overkill" approach correct. – Zophikel Jun 18 '17 at 15:54

2 Answers2

1

$$\sum_{k=1}^n\sin{k}=\frac{\sum\limits_{k=1}^n2\sin\frac{1}{2}\sin{k}}{2\sin\frac{1}{2}}=\frac{\sum\limits_{k=1}^n\left(\cos\left(k-\frac{1}{2}\right)-\cos\left(k+\frac{1}{2}\right)\right)}{2\sin\frac{1}{2}}=\frac{\cos\frac{1}{2}-\cos\left(n+\frac{1}{2}\right)}{2\sin\frac{1}{2}}.$$

Michael Rozenberg
  • 194,933
  • How did you manipulate the sum on the far RHS side. – Zophikel Jun 18 '17 at 15:52
  • @Zophikel I used $\sin\alpha\sin\beta=\frac{1}{2}\left(\cos(\alpha-\beta)-\cos(\alpha+\beta)\right)$. – Michael Rozenberg Jun 18 '17 at 15:54
  • Ahhh ok you just applied a Trig Identity and "Telescoped" from there, also was my initial approach correct despite it being "Overkill", the book I was reading wanted to reader to use Fourier Methods developed in the previous chapters. – Zophikel Jun 18 '17 at 15:56
1

You can also write $$series = Im\bigg( \sum_{k=1}^n e^{ikx}\bigg) =Im\bigg( e^{ix} \frac{1- e^{inx}}{1-e^{ix}} \bigg)= Im \bigg( e^{ix/2} \frac{1- e^{inx}}{e^{-ix/2} - e^{ix/2}} \bigg)\\ = Im \bigg(i \frac{e^{ix/2}- e^{i(n+0.5)x}}{2 \sin(x/2)} \bigg)= Re \bigg( \frac{e^{ix/2}- e^{i(n+0.5)x}}{2 \sin(x/2)} \bigg)= \frac{\cos(x/2) - \cos[(n+0.5)x]}{2 \sin(x/2)} $$

where Im and Re stand for imaginary and real parts of exponential function.

user440429
  • 781
  • Interesting so managed to get the series on the RHS, side of the original conjecture as a Fourier series and then took the real and imaginary parts, could you how you managed to do this. I was another method of doing this and applying Theorem $(3.23)$ would just be useless since we can just get the Fourier representation of our function and just go from there. Now note thatone could just apply the $(3.23)$ and just ignore the integral – Zophikel Jun 18 '17 at 16:28
  • $$[ \sigma_{N} = \sin(x) + (1 - 1/k) \sin(2x) + \cdot \cdot \cdot + (1 - n/k) \sin(n(x)) + \cdot \cdot \cdot \frac{1}{k}\sin(n(x))_{k-1} \tag{1.1}] $$

    $$[\frac{1}{b-a}\int_{a}^{b}\sin(x) + (1 - 1/k) \sin(2x) + \cdot \cdot \cdot + (1 - n/k) \sin(n(x)) + \cdot \cdot \cdot \frac{1}{k}\sin(n(x))_{k-1} e^{2 \pi inx/b-a} \tag{1.1}] $$

    The Fourier Series of $\sigma_{n}$ would be given by: $$\sum_{}^{} \sigma_{n}e^{2 \pi inx/b-a}$$ What would be the bounds of integration ?

     – Zophikel Jun 18 '17 at 16:52