Tangent/normal to a curve - 90 degrees??

Question

I was just plotting $y=x^2$ at the tangent and normal at $x=2$ and noticed that the lines did not even look perpendicular in the slightest. Am I missing something?

For some reason, it's not letting my upload the image. Here's the link (scroll to the plot).

You could evaluate the derivative at x=2. The slope for the normal line is then the negative reciprocal — Daniel H. Hartman, Jun 29 '17 at 21:17
@Daniel Yes, I understand that, but I don't get why it's not showing it at 90 degrees! — PhysicsMathsLove, Jun 29 '17 at 21:18
@PeldePinda Does that make a difference to the angle they intersect at? — PhysicsMathsLove, Jun 29 '17 at 21:18
No, but it does in the picture. I'm having trouble letting wolfram plot it with equal axes, but if you draw it on paper, you'll see that they do in fact intersect at 90 degrees — user388557, Jun 29 '17 at 21:22

score 6 · Accepted Answer · answered Jun 29 '17 at 21:34

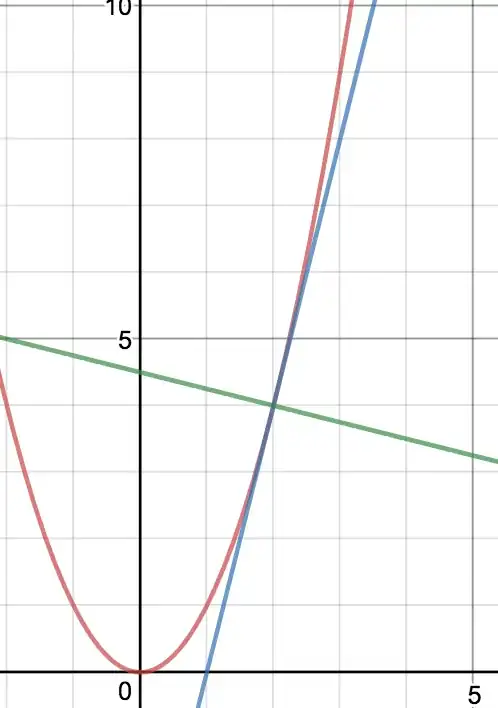
As was pointed out in the comments, the issue is not that the angle is wrong, it's that it really only makes sense to talk about angles on graphs when the axes are scaled the same way. For example, here is everything plotted with the same scale for $x$ and $y$. Note the nice right angles.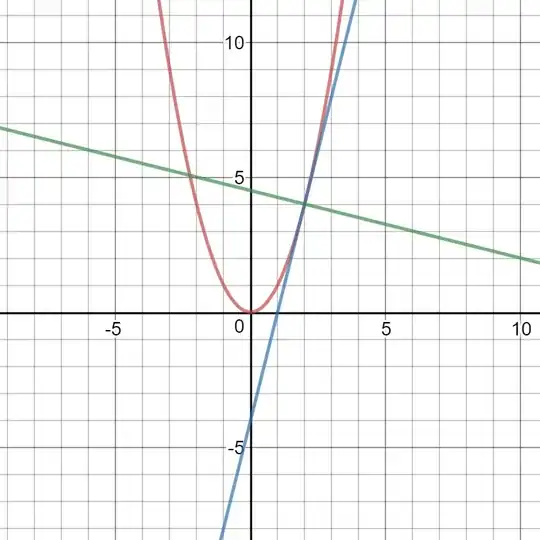

When I change the scale of one of the axes the angles on the graph will change, but that is only an artifact of stretching or compressing in either direction. The tangent line and the normal line will not change, so in particular their slopes will not change, and so they will still be perpendicular. If we defined perpendicular in terms of how lines are drawn on a graph then the concept would not be well defined unless we added the condition that the axes have the same scale. Here's what it looks like with different scales: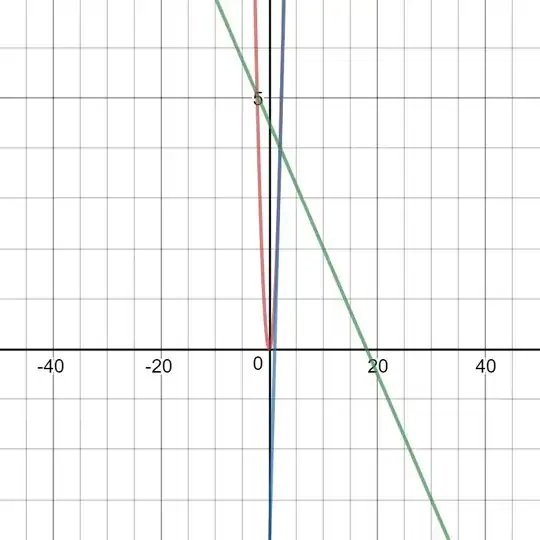 Also, here's the link to the Desmos graph.

score 1 · Answer 2 · answered Jun 29 '17 at 21:37

1

This is simply due to the scaling of the axes. Notice how the $y$-axis increments by 5 and the $x$-axis by 1. See the desmos plot below or here that shows the same two lines are indeed perpendicular.

answered Jun 29 '17 at 21:37

Dando18

5,368

Tangent/normal to a curve - 90 degrees??

2 Answers2