This is not a complete answer to this question however I believe it can bring some insight to this problem. Let us compute the definite integral rather than the antiderivative. Therefore the objective is to compute:
\begin{eqnarray}
{\mathcal I}(a,b):=\int\limits_0^1 \exp\left( -\frac{1}{2} \frac{a+b t}{1-t^2}\right) \frac{1}{\sqrt{1-t^2}} dt
\end{eqnarray}
Firstly let us handle the case $b=0$. In here we substitute for $u=\sqrt{a/2 \cdot t^2/(1-t^2)}$. We have:
\begin{eqnarray}
{\mathcal I}(a,0)&=&\sqrt{2 a} \exp\left(-\frac{a}{2}\right) \frac{1}{4} \int\limits_{-\infty}^\infty \frac{e^{-u^2}}{u^2+a/2} du \\
&=&\sqrt{2 a} \exp\left(-\frac{a}{2}\right) \frac{1}{4} \int\limits_{-\infty}^\infty \frac{e^{-\frac{k^2}{4}}}{\sqrt{2}} \cdot \frac{\sqrt{\pi}}{\sqrt{a}} e^{-\frac{\sqrt{a} |k|}{\sqrt{2}}} dk\\
&=& \frac{\pi}{2} Erfc[\frac{\sqrt{a}}{\sqrt{2}}]
\end{eqnarray}
where in the second line we used the Parseval's identity and in the last line we completed to square and used Gaussian integration.
Now we are going to compute the whole quantity ${\mathcal I}(a,b)$ by expanding the exponential in a series. So we have:
\begin{eqnarray}
{\mathcal I}(a,b)-{\mathcal I}(a,0)&=&\sum\limits_{n=1}^\infty \frac{(-b/2)^n}{n!} \int\limits_0^1
\exp\left( -\frac{1}{2} \frac{a}{1-t^2}\right) \frac{1}{\sqrt{1-t^2}} \left(\frac{t}{1-t^2}\right)^n dt\\
&=&
\sum\limits_{n=1}^\infty \frac{(-b/2)^{2 n}}{(2 n)!} \int\limits_0^1
\exp\left( -\frac{1}{2} \frac{a}{1-t^2}\right) \frac{1}{\sqrt{1-t^2}} \left(\frac{t}{1-t^2}\right)^{2 n} dt+\\
&&\sum\limits_{n=0}^\infty \frac{(-b/2)^{2 n+1}}{(2 n+1)!} \int\limits_0^1
\exp\left( -\frac{1}{2} \frac{a}{1-t^2}\right) \frac{1}{\sqrt{1-t^2}} \left(\frac{t}{1-t^2}\right)^{2 n+1} dt\\
&=&
\sum\limits_{n=1}^\infty \frac{(-b/2)^{2 n}}{(2 n)!} 2^{2 n-1/2} \frac{\sqrt{a} }{a^{2 n}} \exp(-a/2) \sum\limits_{p=0}^{n-1} \binom{n-1}{p} (a/2)^{n-p-1} \frac{1}{2} \Gamma(\frac{1}{2}+n+p) +\\
&&\sum\limits_{n=0}^\infty \frac{(-b/2)^{2n+1}}{(2n+1)!} 2^{2 n+1/2} \frac{\sqrt{a}}{a^{2 n+1}} \sum\limits_{p=0}^n \binom{n}{p} (-a/2)^{n-p} \frac{1}{2} \Gamma(\frac{1}{2}+n+p,\frac{a}{2})
\end{eqnarray}
where the last two lines were derived by substituting for $u$ as on the very top of this answer.
Now we need to check convergence . As it turns out for the series to converge $a$ has to be positive and large enough. Below I plot the integral in question both analytically (from the series expansion) and numerically (from definition).
vals0 = N[Range[1, 2, 1/10]];
vals = N[Range[-1, 1, 1/20]];
myGrid = Flatten[Outer[{#1, #2} &, vals0, vals], 1];
myVals = (1/2 \[Pi] Erfc[Sqrt[#[[1]]]/Sqrt[2]] +
Sum[(-#[[2]]/2)^(2 n + 0)/(2 n + 0)! 2^(2 n -
1/2) Sqrt[#[[1]]]/#[[1]]^(2 n + 0) Exp[-#[[1]]/2] Sum[
Binomial[n - 1, p] (#[[1]]/2)^(-1 + n - p) 1/
2 Gamma[1/2 + n + p], {p, 0, n - 1}], {n, 1, M}] +
Sum[(-#[[2]]/2)^(2 n + 1)/(2 n + 1)! 2^(2 n +
1/2) Sqrt[#[[1]]]/#[[1]]^(2 n + 1) Sum[
Binomial[n, p] (-#[[1]]/2)^(n - p) 1/
2 Gamma[1/2 + n + p, #[[1]]/2], {p, 0, n}], {n, 0,
M - 1}]) & /@ myGrid;
myVals1 =
NIntegrate[
Exp[-1/2 (#[[1]] + #[[2]] t)/(1 - t^2)] 1/Sqrt[1 - t^2], {t, 0,
1}] & /@ myGrid;
(*N[Transpose[{myGrid,myVals,myVals1}]]//MatrixForm*)
pl1 = ListContourPlot[Flatten[#] & /@ Transpose[N[{myGrid, myVals}]],
ContourLabels -> True, ImageSize -> 500,
PlotLabel -> "Analytically"];
pl2 = ListContourPlot[Flatten[#] & /@ Transpose[N[{myGrid, myVals1}]],
ContourLabels -> True, ImageSize -> 500,
PlotLabel -> "Numerically"];
GraphicsGrid[{{pl1, pl2}}]

As we can see the agreement is pretty good once $a\ge 1$.
Update: Let us now compute the antiderivative. We define:
\begin{equation}
{\mathcal I}_{(a,b)}(x):= \int\limits_0^x \frac{1}{\sqrt{1-t^2}} \exp\left(-\frac{1}{2} \frac{a+b t}{1-t^2} \right) dt
\end{equation}
where $x \in(0,1]$.
Now, by doing the same calculations as before with no modification whatsoever we get the following results. Firstly we have:
\begin{equation}
{\mathcal I}_{(a,0)}(x):= 2 \pi T(\sqrt{a}, \frac{x}{\sqrt{1-x^2}})
\end{equation}
where $T$ is the Owen's T function https://en.wikipedia.org/wiki/Owen%27s_T_function .
Then we have:
\begin{eqnarray}
&&\int\limits_0^x \frac{1}{\sqrt{1-t^2}} \exp\left( -\frac{1}{2} \frac{a+b t}{1-t^2} \right) \cdot \left( \frac{t}{1-t^2} \right)^{2 n} dt = \\
&&2^{-1/2+n} a^{1/2-2 n} \sum\limits_{p=0}^{n-1} \binom{n-1}{p} a^{n-1-p} 2^p \exp(-a/2) \Gamma\left(\frac{1}{2} + n+p,0, \frac{a}{2} \frac{x^2}{1-x^2} \right)\\
&&\int\limits_0^x \frac{1}{\sqrt{1-t^2}} \exp\left( -\frac{1}{2} \frac{a+b t}{1-t^2} \right) \cdot \left( \frac{t}{1-t^2} \right)^{2 n+1} dt = \\
&&2^{-1/2+n} a^{-1/2-2 n} \sum\limits_{p=0}^n \binom{n}{p} (-a)^{n-p} 2^p \Gamma\left(\frac{1}{2} +n+p,\frac{a}{2},\frac{a}{2} \frac{1}{1-x^2} \right)
\end{eqnarray}
We can now sum over $n$ to obtain the whole result. It turns out that the series converge quite rapidly. Below I present the contour plots of the quantity in question being computed for $x=0.1,0.3,0.5,0.7,0.9$ from the bottom to the top respectively. As before on the left I produce the analitical result (the series expansion in $n$ being truncated at $n\le 20$) and on the right I show the numerical result (the integral being computed numerically).
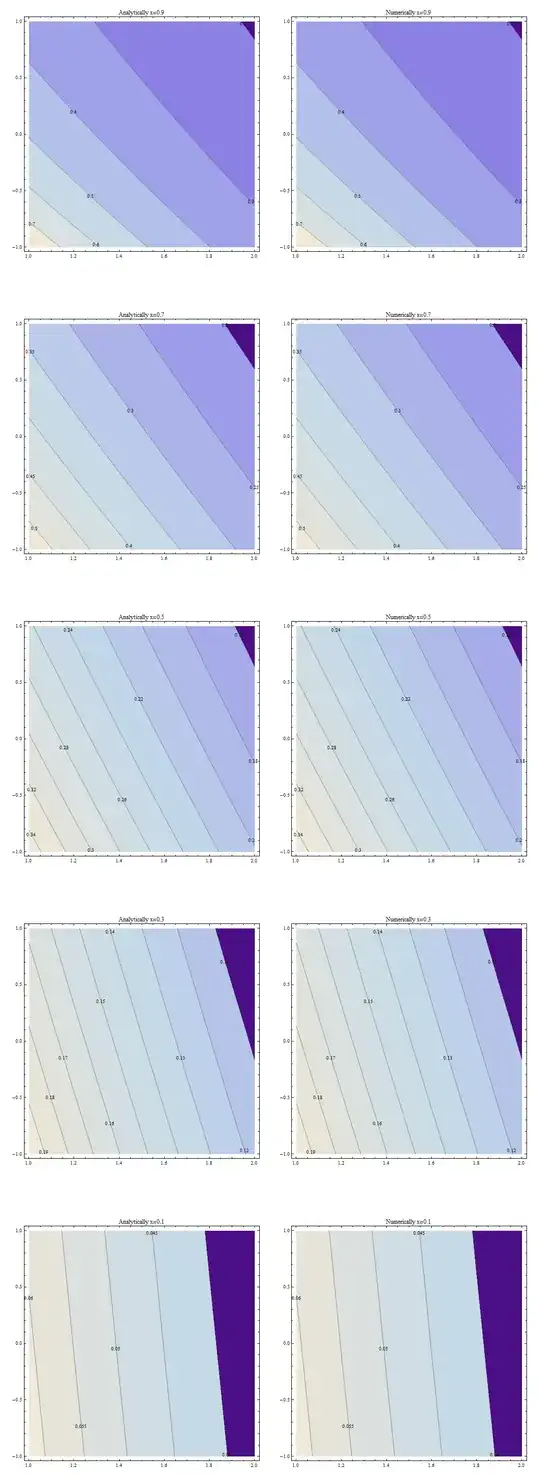
As we can see the agreement is good.

