In the below figure, ABGH, BCFG, CDEF are squares with same length. I need to find $ \alpha + \beta $
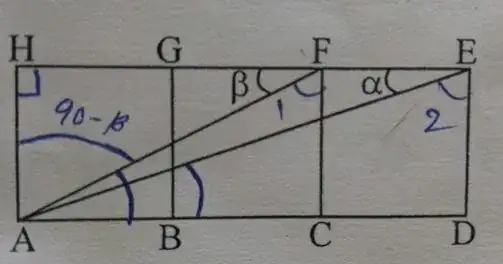
I spend an hour with this and found that answer is 90° but according to answer key, it's 45°. Please help.
In the below figure, ABGH, BCFG, CDEF are squares with same length. I need to find $ \alpha + \beta $

I spend an hour with this and found that answer is 90° but according to answer key, it's 45°. Please help.
It is: $$\tan(\alpha+\beta)=\frac{\frac13+\frac12}{1-\frac16}=1 \Rightarrow \alpha+\beta=45^0.$$
Reflect $E$ and $H$ across line $AD$, you get new points $E',H'$.
Then $\angle AE'H' = \alpha$ since $\triangle AH'E' \cong \triangle AHE$
and
$\angle FE'E =\beta$ and $FE = FA$ since $\triangle FE'E \cong \triangle AFH$.
Since $\angle E'FE = 90^{\circ}-\beta$ we have $\angle AFE' = 90^{\circ}$.
So $\angle AE'F = (\angle FAE') = 45^{\circ}$.
Finally $\alpha +\beta = \angle H'E'E - \angle AE'F = 90^{\circ}- 45^{\circ} = 45^{\circ}$.