2

I have already read one similar question on this topic but I can't use Riemann sums to prove that as instead is done here. The only thing I can use is the definition of $ln(x) = \int^x_1\frac1tdt$ and the known properties of logarithm (i.e. $ln(xy) = ln(x)+ln(y), ln(a^n) = nln(a)$) and properties of integrals.

My book is terrible about it: it just exposes this:

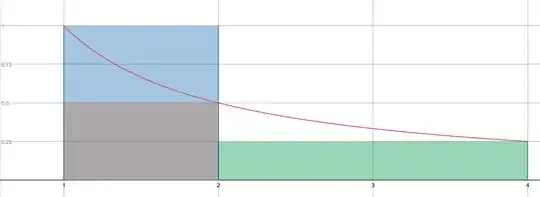
$2 < e < 4$, in fact $\frac12 < ln(2)$ (even this I don't get why) $< 1 = \int^2_11dt$ (for monotony of integrals) $< 2ln(2) = ln(4)$ without explaining why $\frac12 < ln(2)$ and $1 < 2ln(2)$. If you could please give me some info about this I would really love you. (mostly about $ 1 < 2ln(2) $ ).

Thanks.

Baffo rasta
  • 403
  • 1
    If you can use the definition of log as an integral, then the argument with rectangles in the link you've provided is the simplest possible. Just don't call it Riemann sums. – lhf Aug 24 '17 at 23:30

3 Answers3

5

Let's prove that $\ln 2 < 1 < \ln 4$.

Consider the graph of $\dfrac1x$.

The rectangle $[1,2] \times [0,1]$ contains the area of the graph for $x \in [1,2]$. Therefore, $\ln 2 < 1$.

The rectangles $[1,2] \times [0,\dfrac12]$ and $[2,4] \times [0,\dfrac14]$ are contained in area of the graph for $x \in [2,4]$. Therefore, $\ln 4 > 1$.

enter image description here

lhf
  • 216,483
2

From the definition of $\log x = \int_1^x \frac{dt}{t}$, fundamental theorem of calculus tell us

$$\frac{d}{dx}\log(x) = \frac{d}{dx}\int_1^x \frac{dt}{t} = \frac{1}{x}$$

If one define $e$ to be the number such that $\log(e) = 1$, one must have $e > 1$ because the integrand $\frac{1}{t}$ is positive. Furthermore, since the derivative is positive, we have $\log(x) < 1$ when $x < e$ and $\log(x) > 1$ when $x > e$.

Consider the function $\frac{\log(x)}{x}$ for $x \ge 1$, we have:

$$\frac{d}{dx}\left(\frac{\log x}{x}\right) = \frac{1-\log(x)}{x^2} \begin{cases} > 0, & x < e\\ = 0, & x = e\\ < 0, & x > e \end{cases} $$ So the function $\frac{\log x}{x}$ is strictly increasing on $[1,e]$ and strictly decreasing on $[e,\infty)$.

Since $2 \ne 4$ but $$\frac{\log(4)}{4} = \frac{\log(2 \times 2)}{4} = \frac{2\log(2)}{4} = \frac{\log(2)}{2}$$ $2$ and $4$ need to fall into different intervals $[1,e]$ and $[e, \infty)$. Furthermore, none of them can equal to $e$. Together with $2 < 4$, we obtain $$2 \in [1,e),\;4 \in (e, \infty)\quad\iff\quad 2 < e < 4 $$

Math Lover
  • 15,153
achille hui
  • 122,701
0

$\frac 1t < 1$ for $t >1$ so $\ln 2=\int\limits_{1}^2 \frac 1 dt <1*[2-1]=1$

$\frac 1t >\frac 12$ for $1 <t <2$ and $\frac 1t > \frac 14$ for $2\le t <4$, so $\ln 4=\int\limits_{1}^4 \frac 1 dt >\frac 14*[2-1]+\frac 14 [4-2]=1$.

Finally note that as $\frac 1t >0$ for all positive $t $, $\ln $ is monotonically increasing.

So $\ln 2 < 1=\ln e < \ln 4$ we know $2 < e < 4$.

fleablood
  • 124,253